Résumés
Résumé
Malgré une importante demande de recevoir des informations diagnostiques sur les difficultés en lecture des élèves, il existe très peu d’outils d’évaluation conçus spécifiquement pour cet usage. Plusieurs recherches en approche diagnostique cognitive (ADC) utilisent donc les résultats d’épreuves à grande échelle pour fournir de la rétroaction diagnostique fine et fiable sur les forces et les faiblesses des élèves. Les modélisations de données permettent de s’éloigner des scores ou des rangs percentiles habituellement obtenus, et de fournir des pistes d’intervention appropriées. Cette étude vise à vérifier la faisabilité d’appliquer des modélisations à visée diagnostique aux résultats de 4762 élèves canadiens ayant fait le cahier 13 du test du PIRLS de 2011. Les résultats suggèrent un potentiel de recevoir de la rétroaction diagnostique détaillée de leurs forces et faiblesses sur les habiletés sous-jacentes du test.
Mots-clés :
- approche diagnostique cognitive (ADC),
- lecture,
- DINA,
- G-DINA,
- modèles de classification diagnostique (MCD),
- épreuves à grande échelle
Abstract
Despite the grand demand to receive diagnostic information about students’ difficulties in reading, there are very few tests specifically designed for diagnostic purposes. Therefore, many researches in cognitive diagnostic approach (CDA) use large-scale test results to provide fine and reliable diagnostic feedback on the strengths and weaknesses of students other than the total scores or percentiles ranks, which allow appropriate intervention. This study shows an example of the application of diagnostic modeling using data from 4,762 Canadian students who completed booklet 13 of the PIRLS test in 2011. The results highlight the potential for detailed diagnostic feedback of students’ strengths and weaknesses on the underlying skills identified in the test.
Keywords:
- cognitive diagnostic approach (CDA),
- reading,
- DINA,
- G-DINA,
- diagnostic classification models (DCM),
- large-scale tests
Resumo
Apesar da importante procura por informações diagnósticas sobre as dificuldades de leitura dos alunos, existem muito poucas ferramentas de avaliação concebidas especificamente para este uso. Diversas investigações em abordagem de diagnóstica cognitiva (ADC) utilizam, portanto, os resultados de testes em larga escala para fornecer feedback diagnóstico detalhado e fiável sobre os pontos fortes e fracos dos alunos. As modelizações de dados torna possível afastar-se das pontuações ou dos níveis percentuais normalmente obtidos e fornecer pistas de intervenção apropriadas. Este estudo tem como objetivo verificar a viabilidade da aplicação da modelização diagnóstica aos resultados de 4.762 alunos canadianos que realizaram o caderno 13 do teste do PIRLS de 2011. Os resultados realçam o potencial para um feedback diagnóstico detalhado dos pontos fortes e fracos dos alunos em relação às habilidades subjacentes ao teste.
Palavras chaves:
- abordagem diagnóstica cognitiva (ADC),
- leitura,
- DINA,
- G-DINA,
- modelos de classificação diagnóstica (MCD),
- testes em larga escala
Corps de l’article
Introduction
Les demandes en lien avec le diagnostic des difficultés d’apprentissage des élèves ont grandement augmenté ces dernières années (de la Torre, 2009 ; Jang, 2009). Toutefois, très peu d’outils ont été conçus spécifiquement pour cet usage (Alderson, 2010 ; Jang, 2009 ; Lee et Sawaki, 2009 ; Leighton et Gierl, 2007). Plusieurs recherches en approche diagnostique cognitive (ADC) modélisent donc des résultats d’épreuves standardisées à grande échelle comme le Test of English as a Foreign Language (TOEFL), le TOEFL Internet-based Test (iBT) ou la Michigan English Language Assessment Battery (MELAB) pour obtenir de la rétroaction diagnostique fine et fiable sur les forces et les faiblesses des élèves, ce qui permet d’identifier des pistes d’intervention appropriées (Gierl, Cui et Hunka, 2008 ; Hartz, 2002 ; Jang, 2005 ; Templin et Henson, 2006). D’autres études (Dogan et Tatsuoka, 2008 ; Im et Park, 2010 ; Lee, Park et Taylan, 2011 ; Toker et Green, 2012 ; Lee, Park, Sachdeva, Zhang et Waldman, 2013 ; Arican et Sen, 2015 ; Yamaguchi et Okada, 2018) s’intéressent à analyser des données des tests à grande échelle internationaux comme la Trends in International Mathematics and Science Study (TIMSS) avec les modèles de classification diagnostique (MCD) basés sur une matrice, appelée matrice Q, qui relie les items aux connaissances ou habiletés. Ces études fournissent donc des informations détaillées sur la maîtrise des compétences des élèves, sur le lien entre l’enseignement et la performance des élèves, sur le système éducatif des pays et sur leur curriculum (Arican et Sen, 2015).
Dans le domaine des langues, les recherches dans cette approche montrent la possibilité de décomposer la compétence en lecture en un ensemble de connaissances et d’habiletés possibles à diagnostiquer grâce à des modélisations psychométriques (Jang, 2005 ; Leighton et Gierl, 2007). Toutefois, jusqu’à présent, les recherches réalisées en langues n’utilisent que des tests passés aux adultes comme le TOEFL, le TOEFL iBT ou la MELAB. Rares sont les études qui choisissent un test en lecture destiné aux élèves du primaire, soit la tranche d’âge qui nécessite pourtant le plus des pistes d’intervention, étant donné l’influence de cette compétence sur leur réussite scolaire future (Desrosiers et Tétreault, 2012 ; Pagani, Fitzpatrick, Belleau et Janosz, 2011).
S’inscrivant dans le même contexte que la TIMSS, le Programme international de recherche en lecture scolaire (PIRLS) encadre une épreuve qui vise à dégager les tendances dans le rendement en lecture des élèves de 4e année du primaire (Labrecque, Chuy, Brochu et Houme, 2012). Bien que les résultats du test du PIRLS nous renseignent sur la performance des élèves relativement à deux objectifs et à quatre processus en lecture, le Conseil des ministres de l’Éducation du Canada (CMEC) ne communique aucun résultat à titre individuel à l’élève (Labrecque et al., 2012). Ces résultats sont utilisés principalement à des fins de recherche, ce qui limite leur exploitation et leur utilisation pour améliorer l’enseignement et l’apprentissage en lecture au primaire.
L’épreuve en anglais du PIRLS 2011 contient au total 10 extraits de textes, dont 5 textes littéraires et 5 textes informatifs. Six extraits proviennent des épreuves des cohortes précédentes, tandis que quatre extraits ont été nouvellement élaborés pour le test de 2011 (Labrecque et al., 2012). Au total, il y a 135 items, dont de 13 à 16 items pour chaque extrait qui sont répartis de façon quasi égale entre des questions à choix multiples et des questions à court développement (Labrecque et al., 2012). Les extraits et les items ont été divisés en 10 blocs de 40 minutes, puis ont été organisés en 13 cahiers selon un arrangement systématique. Les 13 cahiers se distinguent donc par la combinaison des extraits de texte et des items associés. En effet, cette combinaison systématique assure une répartition équilibrée du type de texte, des types de questions ainsi que du nombre de questions par objectif et par processus en lecture. Elle assure donc une équivalence du contenu entre les différents cahiers de l’épreuve.
À chaque cohorte, le contenu de seulement 10 % des passages et des items a été publié, ce qui permet aux chercheurs d’y accéder pour faire des études. Parmi les cahiers du test de 2011, le cahier 13 a le plus grand nombre de participants, soit 20,7 % des élèves, tandis que les autres cahiers contiennent chacun seulement 6,6 % des élèves. En raison du plus grand nombre de participants du cahier 13 et de l’accès aux contenus des items, des textes et des réponses des élèves, nous avons décidé d’analyser les données de 4762 élèves canadiens ayant fait ce cahier.
Cet article a donc pour but de vérifier la faisabilité d’appliquer des modélisations à visée diagnostique aux résultats des élèves ayant fait le cahier 13 du test du PIRLS 2011. Plus précisément, nous visons trois objectifs spécifiques : 1) évaluer l’ajustement des modèles aux données avec les deux matrices Q, 2) évaluer la qualité diagnostique des items du test du PIRLS et 3) examiner les profils de maîtrise et de non-maîtrise des habiletés de 4762 élèves canadiens ayant fait le cahier 13.
Revue de littérature
Lien entre le test du PIRLS et les modèles théoriques en lecture
Dans le test du PIRLS 2011, la compréhension de l’écrit ou la lecture se définit comme la capacité de comprendre et d’utiliser les formes de la langue écrite exigées par la société et valorisées par l’individu (Labrecque et al., 2012 ; Mullis, Martin, Kennedy, Trong et Sainsbury, 2009). Cette définition se base sur les théories qui articulent la lecture comme un processus « constructif et interactif » (Alexander et Jetton, 2000 ; Anderson et Pearson, 1984 ; Labrecque et al., 2012 ; Mullis et al., 2009). Les élèves sont des « constructeurs actifs » du sens parce qu’ils mobilisent des stratégies cognitives et métacognitives efficaces ainsi que des connaissances linguistiques et des acquis antérieurs pour résoudre les tâches demandées (Afflerbach et Cho, 2009 ; Anderson et Pearson, 1984 ; Carrell, 1983 ; Clay, 1991 ; Langer, 1990). D’ailleurs, la lecture est réalisée dans l’interaction entre le texte et le lecteur dans un contexte particulier qui devrait favoriser l’engagement du lecteur pour répondre aux besoins spécifiques (Giasson, 1996 ; Grabe, 1991 ; Irwin, 1991 ; Mullis et al., 2009 ; Snow, 2002).
Cette vision interactive et constructive fait référence aux modèles interactifs (Rumelhart, 1978), à la théorie du schéma (Anderson et Pearson, 1984 ; Carrell, 1983), au modèle de construction-intégration en lecture (Kintsch, 1988) et au modèle contemporain en lecture (Giasson, 1996 ; Irwin, 1991). Les modèles interactifs (Rumelhart, 1978) distinguent deux types d’interactions : l’interaction entre le lecteur et le texte ainsi que l’interaction entre des habiletés et différents types de connaissances (Carrell, 1983 ; Dubin, Eskey, Grabe et Savignon, 1986 ; Samuels et Kamil, 1984). Dans le premier type d’interaction, les connaissances, les stratégies cognitives et métacognitives, les caractéristiques physiques et motivationnelles du lecteur ainsi que l’interaction de ces caractéristiques influencent le résultat du processus en lecture (Alderson, 2005). Quant aux éléments textuels, le contenu, les types de textes, l’organisation textuelle et la structure des phrases, la typographie, la relation entre le texte verbal et non verbal ainsi que les moyens de présentation du texte facilitent la compréhension de l’élève (Carell, Devine et Eskey, 1988 ; Grabe, 1991).
L’interaction entre les connaissances et les habiletés mobilisées se distingue en différents niveaux, qui varient de la reconnaissance des caractéristiques graphiques des mots à l’interprétation du texte. L’hypothèse principale est que le traitement de l’information se compose en étapes parallèles qui interagissent simultanément et continuellement, plutôt que hiérarchiques, qui se passent les unes après les autres (Carrell et al., 1988). Stanovich (1980) a introduit la notion d’activation dans son modèle interactif compensatoire, qui assume que l’interprétation d’un texte est synthétisée à partir des informations fournies simultanément et provenant de toutes sources de connaissances, et qu’il y a une compensation entre elles, ce qui différencie les lecteurs forts des plus faibles. L’interaction entre les connaissances renvoie également à la théorie du schéma, selon laquelle le texte ne porte pas le sens en lui-même, mais fournit seulement des indications permettant au lecteur de construire du sens à partir de ses propres schémas de connaissances (Adams et Collins, 1979 ; An, 2013). La compréhension efficace d’un texte repose donc sur la capacité de relier les éléments du texte aux connaissances antérieures (An, 2013).
La construction du sens se fait dans les interactions entre le texte, le lecteur et le contexte, comme mentionné dans le modèle contemporain en lecture (Giasson, 1996 ; Irwin, 1991). La compréhension varie selon le degré d’association entre ces trois composantes. Plus elles sont imbriquées les unes aux autres, meilleure sera la compréhension (Giasson, 1996). D’ailleurs, Irwin (1991) classifie les processus en lecture en cinq catégories : 1) les microprocessus, qui servent à comprendre l’information dans une phrase, 2) les processus d’intégration, qui permettent d’établir les liens entre les phrases, 3) les macroprocessus, qui visent la compréhension globale et les liens de cohérence du texte, 4) les processus d’élaboration, qui permettent d’effectuer des inférences, et 5) les processus métacognitifs, qui gèrent la compréhension et amènent le lecteur à s’ajuster à la situation de lecture (Giasson, 1996). Par contre, Kintsch (1988) ainsi que van Dijk et Kintsch (1983), dans le modèle de construction-intégration, distinguent deux niveaux de compréhension : la compréhension globale (la macrostructure), qui porte sur le texte entier, et la compréhension locale (la microstructure), qui concerne la lecture de chaque phrase ou paragraphe.
Cette vision constructive et interactive se traduit en deux objectifs en lecture dans l’épreuve du PIRLS : 1) lire pour l’expérience littéraire et 2) lire pour acquérir et utiliser des informations. À travers des textes narratifs, lire pour l’expérience littéraire (objectif 1) demande aux élèves d’explorer des situations irréelles en apportant au texte leurs propres expériences et sentiments ainsi que l’appréciation du langage et leurs connaissances afin d’interpréter et de créer le sens du texte (Mullis et al., 2009). Ces idées reflètent les caractéristiques fondamentales du modèle de construction-intégration en lecture (Kinstch, 1988) et de la théorie du schéma (Anderson et Pearson, 1984). En lisant pour acquérir et utiliser des informations (objectif 2), les élèves s’impliquent dans les faits réels des textes informatifs pour comprendre le fonctionnement des événements (Mullis et al., 2009). Les différences dans l’organisation et la structure des textes informatifs demandent aux lecteurs d’utiliser diverses stratégies cognitives et métacognitives pour répondre aux tâches demandées, ce qui a été souligné dans les modèles interactifs en lecture (Rumelhart, 1978).
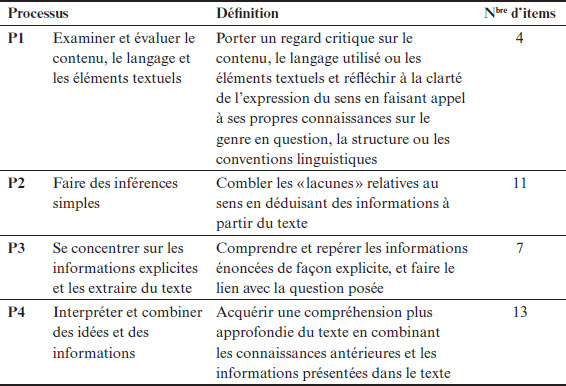
La construction du sens est réalisée dans le test du PIRLS à travers quatre processus en lecture : 1) examiner et évaluer le contenu, le langage et les éléments textuels, 2) faire des inférences simples, 3) se concentrer sur les informations explicites et les extraire du texte et 4) interpréter et combiner des idées et des informations (voir Tableau 1).
Pour se concentrer et récupérer des informations explicites (P3), les lecteurs utilisent différentes façons pour répondre à la question posée en repérant des informations explicitement énoncées dans le texte, ce qui demande une compréhension des phrases sans recourir à l’interprétation ou à l’inférence (Labrecque et al., 2012). Par contre, faire des inférences simples (P2) demande aux élèves d’aller au-delà de la surface du texte et de combler les lacunes en établissant les relations entre les différentes informations (Labrecque et al., 2012 ; Mullis et al., 2009). Ces deux processus font partie d’une compréhension locale.
À l’opposé, afin d’interpréter et d’intégrer les informations dans le texte (P4), les lecteurs établissent des connexions implicites selon leur propre perspective à l’aide de connaissances antérieures, ce qui reflète la théorie du schéma (Anderson et Pearson, 1984). Le niveau de l’intégration et de l’interprétation des informations varie donc selon les expériences et connaissances mobilisées pour les tâches (Labrecque et al., 2012 ; Mullis et al., 2009). Enfin, afin d’examiner et d’évaluer le contenu, la langue et les éléments textuels (P1), les lecteurs doivent prendre du recul par rapport au texte pour porter un regard critique sur le contenu, le langage ou les éléments textuels en se basant sur le genre, la structure ou les conventions linguistiques (Labrecque et al., 2012). Ce processus correspond à la compréhension globale du texte.
Tableau 1
Description des processus et répartition des items
Approche diagnostique cognitive
L’ADC a été développée pendant les années 1980 avec deux composantes principales : 1) l’analyse du contenu des items afin d’identifier les attributs cognitifs sous-jacents et 2) les modèles psychométriques représentant les relations entre ces items et ces attributs (Lee et Sawaki, 2009 ; Yang et Embretson, 2007). Les attributs renvoient à des habiletés, à des connaissances et à des stratégies cognitives que l’élève mobilise pour répondre correctement aux items (Buck et Tatsuoka, 1998 ; Lee et Sawaki, 2009 ; Leighton et Gierl, 2007). En pratique, le diagnostic dans cette approche est réalisé de deux façons. La première façon consiste à analyser les données des tests à grande échelle qui n’ont pas été conçus pour une visée diagnostique en recourant à un modèle cognitif, dans l’espoir d’extraire des informations détaillées sur la maîtrise des habiletés des élèves. La seconde façon consiste à concevoir un test à finalité diagnostique, puis à modéliser les résultats du test pour obtenir des informations diagnostiques (DiBello, Roussos et Stout, 2007).
Notre recherche s’inscrit dans la première approche et passe nécessairement par quatre étapes : 1) l’identification des attributs, 2) la construction d’une matrice Q, 3) la modélisation des données et 4) la rétroaction diagnostique :
L’identification des attributs est souvent réalisée par un panel d’experts en analysant la spécification des tests, le contenu des items, les modèles théoriques sous-jacents et les résultats de recherches empiriques (Lee et Sawaki, 2009 ; Leighton et Gierl, 2007) ;
Une matrice Q est ensuite construite pour représenter les liens entre les attributs identifiés et les items. Cette matrice prend souvent la forme d’un tableau comprenant des chiffres binaires (1 et 0) afin de déterminer si un attribut est nécessaire pour répondre correctement à un item. La construction de la matrice Q peut se baser sur la combinaison entre l’analyse du contenu des items et l’analyse des données empiriques issues d’une passation auprès d’un petit groupe de candidats (Loye et Lambert-Chan, 2016 ; Tjoe et de la Torre, 2014) ou l’analyse des verbalisations à haute voix des candidats (Jang, 2005 ; Li et Suen, 2013) ;
La matrice Q élaborée est intégrée dans la modélisation des données avec les modèles de classification diagnostique (MCD). Ces modèles reposent sur le postulat selon lequel la performance des élèves dépend de la maîtrise ou de la non-maîtrise d’un ensemble d’attributs impossibles à observer directement (Buck et Tatsuoka, 1998) ;
Les modélisations fournissent des résultats sur les paramètres d’items permettant d’évaluer le potentiel diagnostique du test, la qualité de la matrice Q et les paramètres de sujets qui renseignent sur le diagnostic des profils de maîtrise des attributs des élèves (Loye, 2010). Les profils de l’élève sont classés sous forme binaire (0 = non-maîtrise et 1 = maîtrise) selon un point de coupure de 0,5. Ce seuil a été suggéré d’une manière biaisée dans les recherches de Li (2011), Lee et Sawaki (2009) et de la Torre (2009). D’autres recherches (Jang, 2005, 2009) classent les profils sous forme multicatégorielle : non-maîtrise si la probabilité de maîtrise (p) est de 0 à 0,4 ; profil non déterminé (p = 0,41 à 0,6) et maîtrise (p = 0,61 à 1).
Recension des recherches réalisées avec les MCD
Les premières recherches en lecture dans une ADC ont été effectuées avec le modèle de rule-space (Buck, Tatsuoka et Kostin, 1997 ; Kasai, 1997 ; Scott, 1998). Buck et ses collègues (1997) ont analysé les données de 5000 étudiants japonais ayant fait le Test of English for International Communication (TOEIC). Les attributs identifiés se basent sur la taxonomie de sous-habiletés proposée par Grabe (1991) et sur des études empiriques (Freedle et Kostin, 1993). Avec sept attributs retenus, les auteurs peuvent classifier 91 % des candidats dans leurs profils de maîtrise des habiletés et fournir des probabilités de maîtrise pour chaque habileté. Ces scores sont ensuite analysés avec une régression multiple, dont les résultats suggèrent que les attributs peuvent expliquer 97 % de la variation de la performance des candidats. Ainsi, le modèle de rule-space peut expliquer la performance des élèves sur des tâches complexes comme la lecture et leur fournir des informations diagnostiques (Buck et al., 1997). Toutefois, les limites de cette étude résident dans la subjectivité des critères de sélection des attributs. En outre, l’analyse des données est réalisée avec une seule forme du test, ce qui pourrait être fait avec d’autres formats afin de pouvoir comparer les résultats obtenus (Buck et al., 1997).
Jang (2009) a modélisé les données de 2703 candidats du TOEFL iBT avec le modèle de fusion (Hartz, 2002). En analysant les protocoles verbaux des apprenants, les experts ont identifié neuf habiletés, à savoir : 1) déduire le sens d’un mot ou d’une phrase, 2) déterminer le sens d’un mot en utilisant les connaissances antérieures, 3) comprendre les relations entre les parties du texte grâce aux connecteurs logiques, 4) repérer des informations explicites, 5) comprendre des informations implicites, 6) faire des inférences, 7) formuler une négation 8) résumer des idées principales et 9) reconnaître des idées ou des arguments contradictoires. Les habiletés 8, 1, 2 sont les plus maîtrisées par les apprenants, tandis que les habiletés 7 et 9 sont les moins maîtrisées. Ce qui semble intéressant dans cette recherche est que la performance des étudiants au test a été évaluée avant et après avoir suivi des cours préparatoires. Les résultats montrent que leur probabilité de maîtrise des habiletés a été augmentée de 12 % après le cours et qu’environ 85 % des étudiants peuvent améliorer leur performance sur les habiletés.
Ce modèle a été également utilisé pour analyser des données du test de la MELAB dans Li (2011) et Li et Suen (2013). Les attributs identifiés sont basés principalement sur les recherches de Gao (2006) et Jang (2005). Avec les protocoles verbaux, les auteurs ont initialement identifié six attributs, pour les réduire finalement à quatre, vu le nombre insuffisant d’items par attribut, soit : 1) le vocabulaire, 2) la syntaxe, 3) l’extraction des informations explicites et 4) la compréhension des informations implicites. Les résultats suggèrent que les attributs sont globalement maîtrisés par 55 % des élèves. Toutefois, la qualité diagnostique est encore faible chez certains items, car le test n’a pas été conçu spécifiquement pour une visée diagnostique (Li, 2011 ; Li et Suen, 2013).
Lee et Sawaki (2009, 2011) ont mené une étude avec le TOEFL iBT pour diagnostiquer la performance en lecture et à l’écoute avec quatre attributs : 1) comprendre le sens du vocabulaire, 2) comprendre des informations spécifiques, 3) connecter des informations et faire une synthèse et 4) organiser des informations. Les données sont analysées avec le modèle de fusion, le general diagnostic model (GDM) et le modèle des classes latentes (LCM), qui permettent de comparer les profils de maîtrise des candidats. Von Davier (2008) a également appliqué le modèle GDM au TOEFL iBT en analysant deux formats du test, qui traitent à la fois des données dichotomiques et polychotomiques. Avec les quatre habiletés identifiées, les résultats ont démontré l’applicabilité du GDM aux tests à grande échelle en langues.
Dans le contexte des tests internationaux, plusieurs recherches en ADC ont été menées avec des tests en mathématiques, par exemple la TIMSS. Lee, Park et Taylan (2011) ont modélisé les données de 823 élèves de 4e année ayant fait les cahiers 4 et 5 de la TIMSS 2007 avec le modèle deterministic inputs, noisy and gate model (DINA). Au total, 15 attributs ont été identifiés pour le test, qui porte sur 3 domaines : 1) nombre entier, 2) géométrie et 3) affichage des données et interprétation des résultats. Ce même test a été utilisé dans les recherches d’Evran (2019), d’Arican et Sen (2015), de Terzi et Sen (2019), de Toker et Green (2012), de Wafa (2019) et de Wafa, Hussaini et Pazhman (2020). Les résultats des recherches avec un test international comme la TIMSS appuient donc le postulat selon lequel l’ADC offre une plus grande richesse d’information sur la maîtrise des attributs des élèves que les méthodes traditionnelles, ce qui peut être directement utilisé pour améliorer l’enseignement en classe (Lee, Park et Taylan, 2011).
Modèles DINA et G-DINA
Le deterministic inputs, noisy and gate model (DINA) est un modèle non compensatoire qui suppose que le participant doit maîtriser tous les attributs nécessaires pour répondre correctement aux items. Pour chaque item, ce modèle divise les participants en deux classes latentes : 1) ceux qui maîtrisent tous les attributs exigés pour un item (ξij = 1) et 2) ceux qui ne les maîtrisent pas (ξij = 0) (Cui, Gierl et Chang, 2012 ; de la Torre et Douglas, 2008 ; Junker et Sijtsma, 2001). Le modèle tient compte du fait que le participant peut donner une mauvaise réponse, même s’il maîtrise tous les attributs nécessaires (Loye, 2010). Il estime donc deux paramètres : 1) le paramètre de pseudo-chance (gi), qui renvoie à la probabilité qu’un individu puisse répondre correctement à un item, même s’il ne maîtrise pas tous les attributs nécessaires, et 2) le paramètre d’étourderie (si), qui représente la probabilité qu’un individu puisse donner une mauvaise réponse, même s’il maîtrise tous les attributs demandés. Idéalement, ces paramètres devraient être petits pour montrer une grande qualité diagnostique de l’item. Les relations entre ces paramètres sont représentées comme suit :
Ainsi, pour le groupe qui maîtrise tous les attributs, la probabilité de répondre correctement à un item est égale à 1 – si, tandis que, pour ceux qui ne les maîtrisent pas, cette probabilité est égale à gi. Le tableau 2 résume ces probabilités selon les deux groupes latents.
Tableau 2
Probabilités de réponse dans le modèle DINA (adapté de Rupp, Templin et Henson, 2010)
À la différence du DINA, le generalized DINA (G-DINA) ne tient pas compte de la relation restreinte comme conjonctive ou disjonctive des attributs afin de répondre correctement à un item (de la Torre, 2011 ; Ravand, Barati et Widhiarso, 2013). Ainsi, au lieu de séparer les participants en deux classes latentes pour chaque item, le G-DINA les partitionne en 2K*j groupes latents, où K*jest le nombre d’attributs demandés pour l’item j. Chaque groupe représente un vecteur d’attributs réduit α*ij, qui obtient sa propre probabilité de réussite (de la Torre et Douglas, 2008). Le G-DINA présume que, même si les participants ne peuvent pas maîtriser tous les attributs nécessaires (ξij = 0), les probabilités d’obtenir une réponse correcte peuvent varier.
Nous avons choisi ces modèles pour l’analyse des données pour trois raisons. Premièrement, ils sont encore peu utilisés dans le domaine des langues, alors qu’ils sont appliqués avec succès aux données en mathématiques ou issues de simulations (Cui, Gierl et Chang, 2012 ; de la Torre et Douglas, 2008 ; de la Torre, 2011). Deuxièmement, ces modèles sont les plus simples, donc les plus restrictifs et interprétables des MCD qui peuvent traiter des données dichotomiques (de la Torre et Douglas, 2008). En effet, selon DiBello, Roussos et Stout (2007), lors du choix d’un MCD, il faut tenir compte de la faisabilité et de la parcimonie qui sont liées à l’importance de garder les modèles aussi simples que possible en matière de paramètres et d’arriver à un ajustement adéquat des données pour atteindre l’objectif de diagnostic. Finalement, ces modèles peuvent se compenser l’un et l’autre, étant donné que le G-DINA peut combler une limite principale du modèle DINA puisqu’il permet de distinguer les participants en différents niveaux de probabilités de répondre correctement, même s’ils ne maîtrisent pas tous les attributs nécessaires. Par exemple, pour un item qui nécessite trois attributs, le participant qui maîtrise deux attributs a une plus grande probabilité de réussite que celui qui maîtrise un seul attribut (Ravand, Barati et Widhiarso, 2013).
Méthodologie
Cette étude vise à étudier la faisabilité des modélisations à visée diagnostique des données du test du PIRLS 2011. Plus spécifiquement, nous évaluons : 1) l’ajustement des modèles DINA et G-DINA aux données avec les deux matrices Q, 2) la qualité diagnostique des items et 3) les profils de maîtrise des habiletés des élèves.
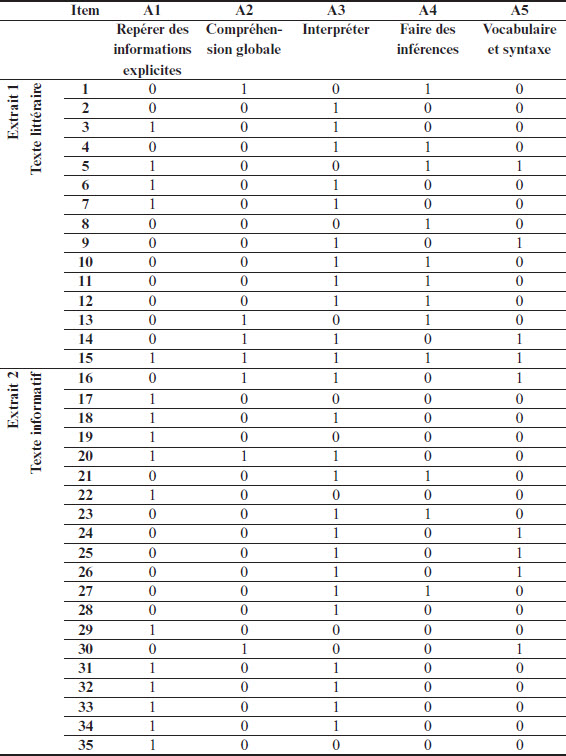
Base de données
Le test est en anglais et se compose de 35 items, répartis en deux sections qui correspondent à deux objectifs de lecture. La première partie porte sur un texte littéraire et contient 16 items, tandis que la seconde partie est un texte informatif avec 19 items. Il y a 15 questions à choix multiples (QCM) avec 4 choix de réponse qui valent un point chacune. Ces questions sont utilisées pour évaluer les processus de compréhension qui ne demandent pas d’évaluation ni d’interprétation complexe. Aussi, 20 items sont à réponse construite à deux points (19 items) ou à trois points (1 item). Ces questions servent à évaluer le processus de l’interprétation (P4), qui exige la mobilisation des connaissances et des expériences antérieures des élèves (Labrecque et al., 2012).
Au Canada, 23 206 élèves ont participé au test du PIRLS 2011, réparti en 13 cahiers. Parmi ceux-ci, 16 500 élèves ont fait le test en anglais, tandis qu’environ 6500 élèves ont fait le test en français (Labrecque et al., 2012). La base de données retenue pour cette recherche contient les réponses de 4762 élèves qui ont fait le livret 13, dont 49,3 % de filles et 50,7 % de garçons. Les réponses des élèves ont été codées dichotomiquement. Les réponses aux QCM sont codées comme 1 (réponse correcte) ou comme 0 (réponse incorrecte). Pour les questions à développement, les réponses de 0 et 1 point sont codées comme 0, tandis que celles de 2 et 3 points sont codées comme 1. Les données manquantes ou les réponses incomplètes sont considérées comme des mauvaises réponses et sont codées comme 0. Cette manière de coder les données a été utilisée dans les recherches avec la TIMSS de Lee, Park et Taylan (2011) et d’Evran (2019).
Participants
Afin d’identifier les attributs sous-jacents du test, un panel d’experts comprenant trois membres a été formé selon trois critères : 1) avoir de bonnes connaissances en langues, 2) avoir des expériences dans l’enseignement des langues et 3) avoir analysé les données de tests de langues à grande échelle à visée diagnostique. Le premier expert a des expériences dans l’élaboration de la matrice Q pour le test du Programme international pour le suivi des acquis des élèves (PISA), tandis que le deuxième est expérimenté dans l’identification des tableaux de spécification pour le test du français pour les immigrants au Québec. Le troisième expert est la cochercheuse elle-même, qui a une formation en didactique des langues et de bonnes connaissances en ADC.
Processus de l’élaboration de deux matrices Q
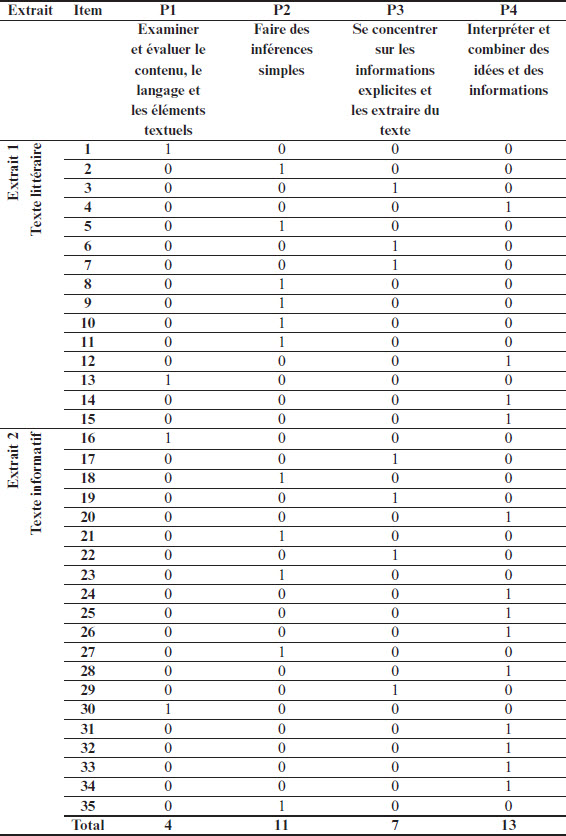
Deux matrices Q ont été élaborées pour notre recherche. Il est à noter que le test du PIRLS a été conçu selon un cadre de référence très bien élaboré avec des modèles cognitifs sous-jacents en lecture. Ce cadre de référence permet d’identifier quatre processus en lecture que les élèves doivent mobiliser pour répondre aux questions, ce qui constitue notre matrice Q1 (voir Tableau 3). L’intérêt est de vérifier si ces processus pourraient être utilisés comme attributs pour des modélisations à visée diagnostique. Cependant, puisque chaque item du test du PIRLS correspond à un seul processus en lecture, cela risque de fournir un diagnostic plus global. Ainsi, nous nous intéressons à savoir s’il est possible de décomposer chaque processus en plusieurs stratégies cognitives en lecture avec le panel d’experts, d’où vient l’idée d’élaborer une matrice Q2 (voir Tableau 5) et de comparer ces deux matrices pour déterminer laquelle fonctionne mieux avec les données. La matrice Q1 a été élaborée par la cochercheuse elle-même à partir de quatre processus de compréhension identifiés dans le cadre de référence du test du PIRLS 2011. Étant donné que chaque item évalue un seul processus de compréhension, les 35 items sont répartis à un seul processus. Le tableau 3 résume la description des processus ainsi que la répartition des items par processus.
Dans cette matrice Q1 (voir Tableau 3), nous constatons une répartition inégale des processus selon les items et les extraits. Par exemple, pour le processus P1, il n’y a que 4 items (11,43 %), dont 2 pour l’extrait 1 et 2 pour l’extrait 2. Par contre, le processus P4 est lié au plus grand nombre d’items : 4 items pour l’extrait 1 et 9 items pour l’extrait 2, donc un total de 13 items (37,14 %). Quant au processus P2, il correspond au total à 11 items (31,43 %), dont 6 items pour l’extrait 1 et 5 pour l’extrait 2. Finalement, 7 items (20 %) sont en lien avec le processus P3, dont 3 items pour l’extrait 1 et 4 items pour l’extrait 2.
Pour la matrice Q2, les experts ont identifié une liste d’attributs sous-jacents pour répondre correctement aux items. La cochercheuse a fourni à chaque expert : 1) le contenu des deux passages, des items et du corrigé, 2) le cadre de référence du test, 3) les informations sur les paramètres d’items et 4) les instructions et les attentes concernant les tâches demandées. Dans un premier temps, l’expert 1 a travaillé en collaboration avec l’expert 3 pour établir une liste d’attributs jugés nécessaires pour l’épreuve. En analysant le contenu des extraits, des questions et du corrigé du cahier 13, les experts ont proposé cinq attributs nécessaires pour le test (voir Tableau 4), certaines questions sollicitant plus d’un processus de compréhension pour répondre à l’item.
Tableau 3
Matrice Q1 élaborée à partir du cadre de référence du test du PIRLS 2011
Par exemple, le processus P4 « Interpréter et combiner des idées et des informations » demande aux élèves de dégager le message ou le thème général d’un texte, de mettre en évidence les points communs et les différences des informations, et d’interpréter les applications possibles des informations dans le monde réel (Labrecque et al., 2012). Ces tâches nécessitent une compréhension globale et une interprétation des idées dans leurs propres mots. Nous avons donc décidé de séparer ce processus en deux attributs : la compréhension globale (A2) et interpréter (A3).
Quant au processus P1 « Examiner et évaluer le contenu, le langage et les éléments textuels », les élèves doivent comparer la signification d’un mot à leur propre compréhension ou aux informations en provenance d’autres sources et réfléchir à la clarté de l’expression du sens, en faisant appel à leurs propres connaissances (Labrecque et al., 2012). Ce processus renvoie à une compréhension globale du texte et aussi à la capacité des élèves à reformuler les idées selon leurs propres mots, ce qui nécessite une bonne maîtrise du vocabulaire et de la syntaxe.
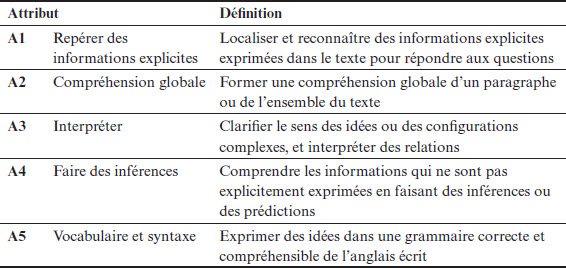
Grâce à l’analyse de l’ensemble des processus en lecture indiqué dans le cadre de référence, les deux experts ont finalement identifié cinq attributs : A1 Repérer des informations explicites, A2 Compréhension globale, A3 Interpréter, A4 Faire des inférences simples et A5 Vocabulaire et syntaxe. Le tableau 4 présente la définition plus détaillée de ces cinq attributs.
Tableau 4
Définitions détaillées des attributs
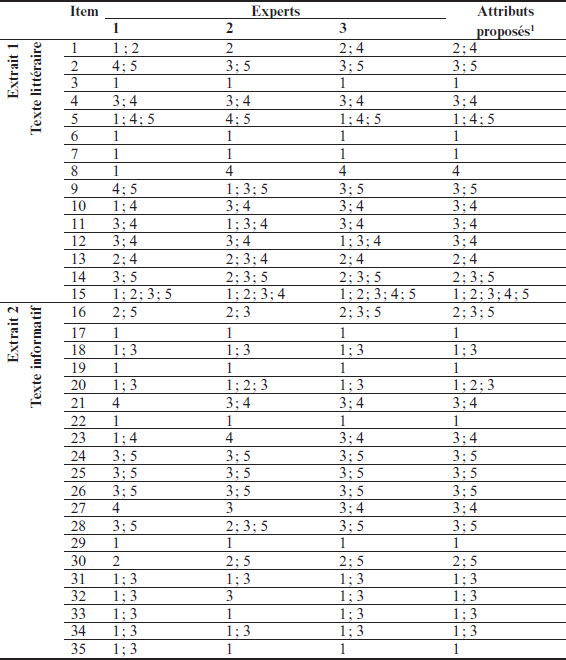
Dans un deuxième temps, les experts ont identifié individuellement les attributs nécessaires pour chaque item. Puisque l’expert 2 n’a pas participé au processus d’identification de la liste d’attributs, nous lui avons demandé d’ajouter d’autres attributs, s’il le jugeait nécessaire. Les experts pouvaient choisir plus d’un attribut par item au besoin. Dans ce cas, ils devaient classer ces attributs par ordre d’importance. Le tableau 5 présente les résultats de l’identification des attributs des experts pour chaque item.
Tableau 5
Matrice Q2 initiale élaborée par les experts
Lors de la remise des résultats, aucun attribut n’a été ajouté par l’expert 2. La statistique de Kappa de Fleiss (1971) a été calculée pour mesurer le degré d’accord interexperts avec le logiciel AgreeStat 2015. Le tableau 6 présente les pourcentages d’items selon le taux de concordance entre les experts. Seuls les items obtenant l’accord d’au moins deux des trois experts (Kappa de Fleiss ≥ 0,6) ont été retenus. Les items avec une plus forte concordance sont de manière logique des items à un seul attribut. Pour les items ayant un taux de concordance faible et moyen, nous avons examiné les commentaires des experts afin de faire les ajustements nécessaires.
Tableau 6
Répartition des items selon le taux de concordance des experts
Les attributs sélectionnés pour chaque item ont ensuite été compilés afin de former une matrice Q2_initiale. Cette matrice a été examinée et raffinée par nos experts afin d’arriver à une matrice Q2_finale, retenue pour les modélisations. Bien que des directives strictes ne soient pas proposées, Hartz (2002) suggère que chaque attribut soit mesuré par au moins trois items et défini au sens large. Ainsi, les attributs qui ne respectent pas ce critère sont combinés soit à un attribut similaire, soit à un attribut éliminé de la matrice Q2_finale. Finalement, la matrice Q2_finale (voir Tableau 7) contient 9 items à un attribut, 21 items à deux attributs, 4 items à trois attributs et 1 seul item à cinq attributs. Les items à un ou deux attributs sont des items à 1 point, tandis que ceux à trois ou à cinq attributs sont de 2 et 3 points.
Tableau 7
Matrice Q2_finale proposée pour des modélisations du test du PIRLS 2011
Analyse
La base de données dichotomiques ainsi que les matrices Q1 et Q2 ont été modélisées avec DINA et G-DINA avec le logiciel OxEdit, qui permet d’évaluer des ajustements relatifs et absolus des modèles aux données, d’estimer des paramètres d’items et d’identifier les profils de maîtrise des habiletés des élèves.
Évaluation de l’ajustement des modèles aux données
L’évaluation de l’ajustement des modèles aux données permet de vérifier la cohérence essentielle entre le modèle estimé (données prédites) et les données observées pour suggérer des améliorations au modèle (DiBello, Roussos et Stout, 2007 ; Sinharay, 2004). Dans l’évaluation de l’ajustement des MCD, nous pouvons distinguer l’évaluation de l’ajustement relatif de celle de l’ajustement absolu. Ainsi, l’évaluation de l’ajustement relatif des MCD renvoie au processus de sélection du modèle le plus approprié parmi des modèles concurrents (Chen, de la Torre et Zhang, 2013). Dans cette étude, les trois statistiques suivantes sont utilisées pour l’évaluation de l’ajustement relatif de DINA et G-DINA :
1) -2 log-vraisemblance (-2LL) : |
-2LL = 2ln (ML) |
2) Critère d’information d’Akaike (AIC) : |
-2LL + 2P |
3) Critère d’information bayésien (BIC) : |
-2LL + P ln(N), |
où ML est le maximum de vraisemblance des paramètres d’items ; P est le nombre de paramètres du modèle ; L est le nombre total de schémas d’attributs et N est la taille de l’échantillon. Pour chaque statistique, le modèle avec la valeur la plus petite sera préféré aux modèles concurrents (Chen, de la Torre et Zhang, 2013).
L’évaluation de l’ajustement absolu des MCD permet de déterminer si les modèles sont ajustés adéquatement aux données. Ainsi, trois statistiques sont utilisées : 1) le résidu entre la proportion d’items corrects prédite et observée, 2) le résidu entre la corrélation transformée de Fisher prédite et observée de chaque paire d’items et 3) le résidu entre le ratio log-odds observé et prédit de chaque paire d’items (Chen, de la Torre et Zhang, 2013). Avec ces trois statistiques, un grand nombre de schémas d’attributs est échantillonné à partir de la distribution postérieure des attributs. Les schémas d’attributs généralisés et les paramètres estimés peuvent être utilisés pour générer les réponses prédites aux items. La différence entre les réponses observées et celles prédites devrait être 0 si le modèle est ajusté aux données de manière adéquate.
Afin d’utiliser ces trois statistiques, nous devons calculer leurs erreurs standardisées (SE), ce qui permet de dériver les scores Z de ces trois statistiques pour vérifier si les résidus sont statistiquement différents de 0. Le rejet de n’importe quel score Z signifie que le modèle ne s’ajuste pas adéquatement à un item ou à une paire d’items (Chen, de la Torre et Zhang, 2013). Nous devons nous baser sur au moins deux des trois indices qui sont statistiquement différents de 0 pour montrer que le modèle choisi s’ajuste adéquatement aux données. Ainsi, cette étape d’évaluation de l’ajustement absolu permet de détecter les erreurs de surspécification ou de sous-spécification des attributs dans la matrice Q.
Évaluation de la qualité diagnostique des items
L’estimation des paramètres de pseudo-chance (g) et d’étourderie (s) permet d’évaluer la qualité diagnostique des items, ce qui est déterminé par 1-g-s. Les seuils pour l’interprétation des paramètres sont souvent biaisés et varient d’un auteur à l’autre. Par exemple, selon de la Torre (2009), ces paramètres peuvent être classés en trois catégories : 0-0,1 = bonne qualité ; 0,1-0,2 = moyenne qualité et 0,2-0,3 = faible qualité. Par contre, selon Ma, Iaconangelo et de la Torre (2016), les items sont classés comme de bonne qualité si ces paramètres se trouvent entre 0 et 0,15 ; de moyenne qualité s’ils sont entre 0,15 et 0,25 ; et de faible qualité s’ils sont entre 0,25 et 0,35. Finalement, selon Ravand, Barati et Widhiarso (2013), les items sont considérés comme de bonne qualité si ces paramètres sont inférieurs à 0,5 et de faible qualité s’ils sont supérieurs à 0,5.
Résultats
Évaluation de l’ajustement relatif et absolu des modèles aux données
Ajustement relatif
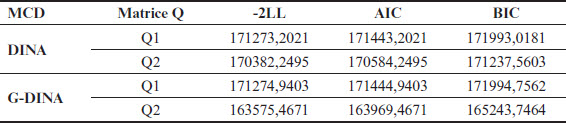
Le tableau 8 présente les résultats de l’évaluation de l’ajustement relatif des modèles aux données avec les indices de -2LL, AIC et BIC. Le modèle ayant les plus petites valeurs sera choisi comme celui qui s’ajuste le mieux aux données. Ainsi, les résultats suggèrent que le modèle G-DINA s’ajuste mieux aux données que le modèle DINA avec la matrice Q2_finale, comparé à la matrice Q1. Plus précisément, avec le DINA et la matrice Q1, les indices sont légèrement inférieurs à ceux avec le G-DINA. Par contre, avec la matrice Q2_finale, le modèle G-DINA s’ajuste mieux que le DINA, étant donné les valeurs plus petites de ces statistiques. Dans les deux modèles, les données s’ajustent mieux avec la matrice Q2_finale qu’avec la matrice Q1. Nous concluons donc que le modèle G-DINA est celui qui s’ajuste le mieux aux données avec la matrice Q2_finale.
Tableau 8
Ajustement relatif des modèles aux données avec les matrices Q1 et Q2_finale
Note. -2LL = -2 log-vraisemblance ; AIC = critère d’information d’Akaike ; BIC = critère d’information bayésien.
Ajustement absolu
Pour l’évaluation de l’ajustement absolu, les statistiques de la proportion correcte (prop.), de la corrélation transformée (Z [Corr]) et du ratio log-odds (Log [OR]) ont été utilisées (Chen, de la Torre et Zhang, 2013) (voir tableau 9). Ces valeurs doivent être proches de 0 pour tous les items afin de montrer que le modèle s’ajuste aux données. Les valeurs maximales des scores Z de ces trois statistiques ont été également dérivées. Les seuils de rejet de ces scores Z ont été également utilisés pour décider si les modèles s’ajustent adéquatement ou non aux données. En principe, ces valeurs doivent être inférieures aux valeurs critiques pour montrer que le modèle retenu s’ajuste adéquatement aux données. Dans le cas contraire, l’ajustement du modèle retenu est rejeté (Ma et Meng, 2014).
Proportion correcte
Pour la proportion correcte (voir Tableau 9), les valeurs maximales des scores Z sont plus ou moins semblables avec les deux matrices dans les deux modèles DINA et G-DINA. Les valeurs maximales des scores Z sont plus petites avec le modèle G-DINA et plus petites avec la matrice Q2_finale. En comparant avec les valeurs critiques des scores Z avec la correction de Bonferroni, ces valeurs obtenues sont toutes inférieures aux valeurs critiques. Nous concluons donc que les deux modèles s’ajustent adéquatement aux données avec tous les items et avec les deux matrices Q.
Tableau 9
Ajustement absolu des modèles aux données avec les matrices Q1 et Q2_finale
Note. Max = valeur maximale des scores Z ; Prop. = proportion correcte ; Z (Corr) = corrélation transformée ; Log (OR) = ratio log-odds. Valeur de score Z critique (Zc) = 3,467 ; 3,649 ; 4,044 pour α = 0,1 ; 0,05 ; 0,01, respectivement (avec la correction de Bonferroni).
Corrélation transformée
Avec la corrélation transformée de Fisher, les valeurs maximales sont proches pour le DINA et le G-DINA avec la matrice Q1. La différence est plus grande entre le DINA et le G-DINA dans la matrice Q2_finale. Selon la proportion correcte (prop.), le modèle G-DINA s’ajuste mieux aux données et il s’ajuste mieux avec la matrice Q2_finale. La comparaison avec des valeurs critiques des scores Z confirme l’ajustement adéquat des deux modèles aux données pour tous les items et avec les deux matrices Q.
Ratio log-odds
Quant aux scores Z du ratio log-odds, les valeurs obtenues sont grandement différentes de celles obtenues avec la proportion correcte et la corrélation transformée, même si nous observons les mêmes tendances, c’est-à-dire que les valeurs sont plus petites avec le modèle G-DINA et plus petites avec la matrice Q2_finale. Cependant, ces valeurs obtenues sont toutes supérieures aux valeurs critiques des scores Z. Nous concluons donc que les modèles DINA et G-DINA ne s’ajustent pas adéquatement aux données avec tous les items.
En comparant ces trois statistiques, nous constatons que les valeurs sont proches entre la proportion correcte et la corrélation transformée dans les deux modèles et avec les deux matrices Q, ce qui aboutit à la même décision de ne pas rejeter l’hypothèse nulle et à conclure qu’il y a de l’ajustement absolu des modèles aux données avec tous les items. Cette décision nous suggère que la sensibilité de ces deux statistiques dans l’évaluation de l’ajustement absolu des données est plus ou moins identique. Par contre, les valeurs du ratio log-odds sont considérablement différentes des deux statistiques précédentes et nous amènent à rejeter l’hypothèse nulle, donc il n’y a pas d’ajustement absolu des modèles aux données avec tous les items. Cette décision nous porte à nous questionner sur la fiabilité et la sensibilité de cette statistique dans l’évaluation de l’ajustement absolu des données.
En résumé, les résultats montrent que le modèle G-DINA s’ajuste mieux que le DINA aux données, et plus avec la matrice Q2_finale que la matrice Q1. Ces modèles s’ajustent adéquatement aux données avec les deux matrices Q selon les statistiques de la proportion correcte et de la corrélation transformée. Cependant, les résultats du ratio log-odds nous indiquent le contraire. Nous nous basons donc sur les résultats de la proportion correcte et de la corrélation transformée, car ces résultats aboutissent à la même décision. À partir de ces résultats, nous examinons les paramètres d’items avec le modèle DINA et les profils de maîtrise des habiletés des élèves obtenus avec la matrice Q2_finale et le modèle G-DINA.
Estimation des paramètres d’items
Pseudo-chance
La moyenne du paramètre de pseudo-chance est de 0,36443 (voir Tableau 10), c’est-à-dire que l’élève a 36,43 % de chance de répondre correctement aux questions, même s’il ne maîtrise pas tous les attributs nécessaires. Selon les critères définis par de la Torre (2009), au titre de pseudo-chance, il y a 6 items de bonne qualité, 3 items de moyenne qualité et 7 items de faible qualité. Au total, 19 items sont problématiques. La plupart des items de bonne et de moyenne qualité se trouvent dans la seconde partie du test. La première partie ne contient que quatre items de moyenne et de faible qualité. Selon les critères de Ravand, Barati et Widhiarso (2013), il y a 23 items de bonne qualité et 12 items de faible qualité en matière de pseudo-chance.
Étourderie
La moyenne du paramètre d’étourderie est de 0,2198 (voir tableau 10). Autrement dit, en moyenne, l’élève a 21,98 % de chance de répondre incorrectement, même s’il maîtrise tous les attributs exigés. D’après les critères définis par de la Torre (2009), au titre de l’étourderie, il y a 13 items de bonne qualité, 4 items de moyenne qualité et 7 items de faible qualité. Finalement, 11 items sont problématiques en matière d’étourderie. Cependant, les seuils de Ravand, Barati et Widhiarso (2013) nous suggèrent qu’il y a seulement 3 items de faible qualité et 32 items de bonne qualité.
Tableau 10
Estimation des paramètres d’items avec la matrice Q2_finale et avec DINA
Pseudo-chance et étourderie
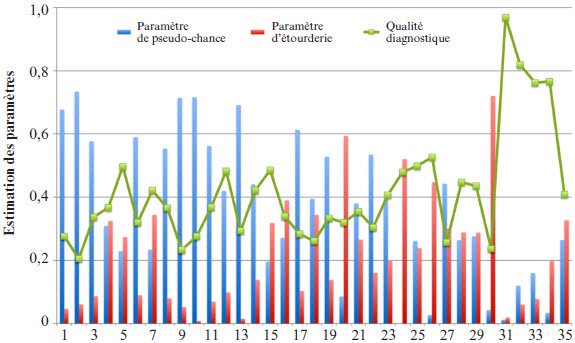
La somme des moyennes des deux paramètres est de 0,5841, ce qui indique que la qualité diagnostique des items est de 0,4259. Selon les seuils définis par de la Torre (2009), il y a seulement deux items de bonne qualité (g+s = 0 à 0,2). Aussi, 2 items sont de moyenne qualité (g+s = 0,2 et 0,4), tandis que 12 items sont de faible qualité (g+s = 0,4 et 0,6). Finalement, il y a 19 items jugés problématiques (g+s > 0,6). La plupart des items se trouvent dans la première partie du test. Cependant, selon les seuils de Ravand, Barati et Widhiarso (2013), il y a 16 items de bonne qualité (g+s < 0,6) et 19 items de faible qualité (g+s > 0,6). La figure 1 présente l’estimation des paramètres d’items et la qualité diagnostique des items. Plus la ligne est élevée, meilleure est la qualité diagnostique des items.
Figure 1
Estimation des paramètres d’items et leur qualité diagnostique
Profil de maîtrise des habiletés des élèves
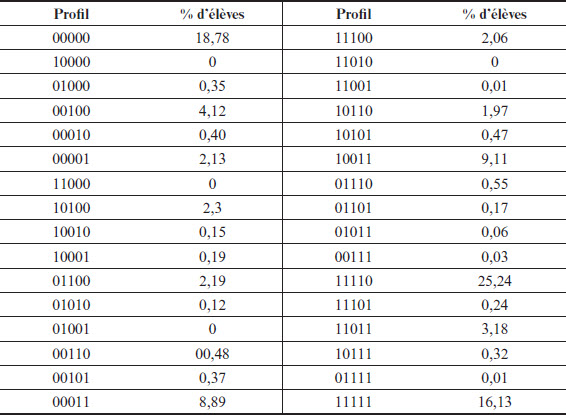
Le tableau 11 présente les 32 profils avec le pourcentage d’élèves correspondant pour chaque profil. Le profil le plus fréquent est 11110 (25,24 %), c’est-à-dire que 25,24 % des élèves maîtrisent les quatre premiers attributs, mais pas le cinquième. Vient ensuite le profil des élèves qui ne maîtrisent aucun des cinq attributs, soit 00000 (18,78 %). Le profil de ceux qui maîtrisent tous les attributs (11111) arrive au 3e rang (16,13 %). Le profil 10011 est aussi présent parmi nos participants avec 9,11 %. Selon ce profil, l’élève a bien maîtrisé les attributs A1 Repérer des informations implicites, A4 Faire des inférences et A5 Vocabulaire et syntaxe, mais pas les attributs A2 Compréhension globale et A3 Interpréter. Le profil 00011 suit de très près avec 8,89 %. Aucun participant ne fait partie d’un des quatre profils suivants : 10000, 11000, 01001 et 11010. Nous donnerons plus d’explications dans la section Discussion.
Tableau 11
Profils et pourcentages des participants
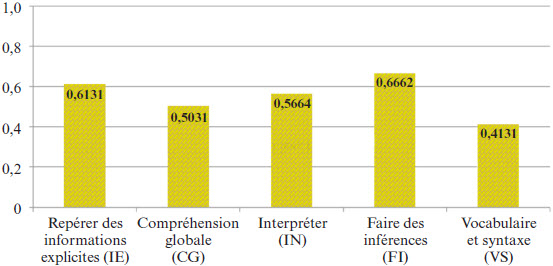
L’attribut A4 Faire des inférences est le mieux maîtrisé (66,62 %). Vient ensuite A1 Repérer des informations implicites (61,31 %). L’attribut A3 Interpréter est classé au 3e rang (56,64 %) des probabilités de maîtrise. L’attribut A2 Compréhension globale est maîtrisé par 50,31 % et, finalement, l’attribut A5 Vocabulaire et syntaxe est le moins maîtrisé (41,31 %). La figure 2 présente les probabilités de maîtrise des attributs pour l’ensemble des élèves.
Figure 2.
Probabilités de maîtrise des attributs pour l’ensemble des élèves
Discussion
Cette étude vise à vérifier la possibilité de modéliser les données de 4762 élèves canadiens du cahier 13 du test du PIRLS 2011 à visée diagnostique. Deux matrices Q ont été élaborées par trois experts. Puis, les données ont été analysées avec le DINA et le G-DINA, ce qui permet d’évaluer l’ajustement des modèles aux données ainsi que d’examiner la qualité diagnostique des items et les profils de maîtrise des attributs des élèves.
Le fait que le modèle G-DINA s’ajuste mieux aux données que le DINA corrobore très bien les résultats des recherches réalisées en mathématiques par Basokcu (2014) et par Ma, Iaconangelo et de la Torre (2016). En effet, le G-DINA assouplit l’hypothèse de la probabilité égale de réponses correctes lorsque les élèves ne maîtrisent pas tous les attributs demandés. Ainsi, même s’ils ne maîtrisent pas tous les attributs, la probabilité d’y répondre correctement peut varier d’un participant à l’autre, vu le nombre et la nature des attributs qui ne sont pas maîtrisés (Loye, 2010).
De plus, le G-DINA est souvent moins influencé que d’autres modèles spécifiques lorsqu’il y a des changements dans les matrices Q (Basokcu, 2014), ce qui est le cas de notre étude (entre Q1 et Q2_finale). Malgré le meilleur ajustement des MCD généralisés, les modèles spécifiques, lorsqu’ils sont utilisés correctement, donnent cependant la possibilité d’obtenir des interprétations plus simples et stables, et de fournir des profils de maîtrise des attributs plus exacts (Ma, Iaconangelo et de la Torre, 2016). Une des suggestions est d’utiliser le test de Wald pour chaque item afin de déterminer si un MCD généralisé peut être remplacé par un MCD spécifique sans perdre la qualité de l’ajustement aux données (Ma, Iaconangelo et de la Torre, 2016). Cependant, nous n’avons pas réalisé cette étape, car cela ne fait pas partie de l’objet principal de notre étude.
Les résultats de la proportion correcte et de la corrélation transformée montrent que les modèles s’ajustent adéquatement aux données, mais pas selon les ratios log-odds. Ainsi, la question sur la fiabilité et la sensibilité de ces statistiques se pose lorsque les trois statistiques n’aboutissent pas aux mêmes décisions (Chen, de la Torre et Zhang, 2013). La recherche suggère qu’il y a probablement des problèmes d’inexactitude dans la matrice Q que nous devons détecter avec des techniques plus sophistiquées, comme le test de Wald. De plus, il est important de vérifier quelle statistique pourrait être fiable dans l’évaluation de l’ajustement absolu selon le MCD utilisé, la nature des réponses ainsi que le type et le nombre d’attributs identifiés. Cet élément a été souligné dans les travaux de Jang (2005, 2009), de Chen, de la Torre et Zhang (2013) et de Ma, Iaconangelo et de la Torre (2016).
L’ajustement est meilleur avec la matrice Q2_finale qu’avec la matrice Q1, ce qui souligne le caractère multidimensionnel de la lecture, car la plupart des items sont liés à au moins deux attributs. En effet, pour la matrice Q1, les 35 items sont des items à un seul attribut, tandis que, dans la matrice Q2_finale, à part les 9 items à un attribut, il y a 26 items de deux attributs et plus. Ce problème d’ajustement souligne donc l’importance du raffinement des attributs dans la matrice Q, car plus ils sont détaillés, plus fines sont les informations diagnostiques obtenues (Lee et Sawaki, 2009 ; Li, 2011). Cette idée est appropriée dans le cas du test du PIRLS 2011 avec la matrice Q1, car les processus P1 Examiner et évaluer le contenu, le langage et les éléments textuels ou P4 Interpréter et combiner des idées et des informations nécessitent d’être séparés en deux attributs, selon les explications que nous avons données dans le processus d’élaboration des matrices Q. Toutefois, un nombre élevé d’attributs peut engendrer des problèmes sur la capacité des modélisations des MCD, un facteur important à considérer autre que la pertinence des profils de maîtrise des attributs.
Ainsi, un défi des concepteurs est de maintenir l’équilibre entre le nombre d’attributs identifiés et la longueur du test, c’est-à-dire qu’il faudrait ajouter plus d’items lorsque le nombre d’habiletés identifiées pour le test est grand (Li, 2011). Parfois, lorsque les conditions sur l’élaboration de la matrice Q sont respectées, la décision sur le choix de la matrice Q renvoie aux résultats fournis par les modélisations. Autrement dit, nous devons laisser les MCD décider quelle matrice Q s’ajuste le mieux aux données, comme nous l’avons fait avec deux matrices Q.
Les paramètres de pseudo-chance et d’étourderie suggèrent une qualité diagnostique moyenne des items, probablement parce que le test n’a pas été conçu avec une visée diagnostique. Cette idée a été clairement confirmée dans les recherches de Li (2011), de Jang (2009), de Ravand, Barati et Widhiarso (2013) et de Huang et Wang (2014).
Par ailleurs, le fait que la qualité diagnostique est meilleure dans la partie 2 du test s’explique par le lien entre l’objectif de la lecture, le type de texte et la qualité psychométrique des items. En effet, l’extrait 2 du test est de nature informative, avec une structure organisationnelle plus claire et cohérente que celui de la partie 1, qui est de nature fictive et vaguement structuré, avec des phrases de conversation entre les personnages. Par ailleurs, plusieurs recherches sur l’influence des éléments textuels et la compréhension en lecture font cette observation (Jang, 2009). Par exemple, Freedle et Kostin (1993) rapportent qu’au moins le tiers (33 %) de la variance de la difficulté de l’item du TOEFL RC est expliqué par des variables associées au contenu et aux structures des passages. Alderson, Percsich et Szabo (2000) soutiennent que la compétence en lecture entraîne la capacité de reconnaître les idées présentées et de comprendre les intentions de l’auteur dans une séquence d’idées. Jang (2009) confirme que les textes avec différentes structures organisationnelles rhétoriques déterminent différents processus cognitifs des élèves.
Les QCM ont un paramètre de pseudo-chance plus élevé que les questions à développement. Cependant, selon Huang et Wang (2014), ce paramètre renvoie non seulement aux caractéristiques des items, mais aussi à l’habileté de l’élève, car la pseudo-chance est l’interaction entre la tendance d’un item qui suscite les devinettes et la capacité à deviner de l’élève. De plus, les élèves compétents peuvent avoir une plus grande capacité à deviner la réponse correctement que ceux moins compétents. Par contre, ceux plus faibles sont facilement influencés par les facteurs de distraction (Huang et Wang, 2014). Ces résultats pourraient être intéressants pour l’identification des attributs, car les variables textuelles peuvent susciter différentes habiletés cognitives, tandis que le choix des types de questions pourrait influencer la qualité diagnostique des items (Jang, 2009).
Les probabilités de maîtrise des habiletés corroborent grandement les théories en lecture et le degré de difficulté des habiletés, car les attributs A1 Repérer des informations implicites et A4 Faire des inférences sont considérés comme plus faciles que A2 Compréhension globale et A3 Interpréter. L’attribut A5 Vocabulaire et syntaxe semble le plus difficile à maîtriser, ce qui a été renforcé par le constat que le manque de vocabulaire est l’obstacle majeur à la compréhension de la lecture (García, 1991 ; Jang, 2009 ; Li, 2011). Une règle de base est que les lecteurs doivent connaître 95 % des mots d’un texte pour lire le texte avec succès (Grabe, 2000 ; Li, 2011). Cependant, bien que l’attribut A1 Repérer des informations explicites soit jugé plus facile que A4 Faire des inférences, il est moins maîtrisé par les élèves, avec 5 % de différence. Selon nous, la complémentarité des attributs dans une question contribue à augmenter la probabilité de maîtrise de l’attribut A4 Faire des inférences. En effet, parmi 16 items reliés à A1 Repérer des informations explicites, la moitié est à un seul attribut. Par contre, seulement 1 item a un attribut parmi les 12 items pour lesquels A4 Faire des inférences a été identifiée. Les 11 items qui restent sont à deux, trois, quatre et cinq attributs.
Le profil le plus représentatif regroupe des élèves qui maîtrisent A1 Repérer des informations explicites, A2 Compréhension globale, A3 Interpréter et A4 Faire des inférences, mais pas A5 Vocabulaire et syntaxe. Ces résultats correspondent bien à nos attentes, car l’attribut Vocabulaire et syntaxe est celui qui représente le plus grand défi, donc il est logique qu’il soit le moins maîtrisé chez les élèves.
Les quatre profils peu probables des élèves s’expliquent par la nature compensatoire des habiletés en lecture :
Le profil 10000, correspondant à l’élève qui ne maîtrise que A1 Repérer des informations explicites, est le moins représenté parce qu’une moitié des questions dans lesquelles cette habileté a été identifiée comme nécessaire est constituée d’items à deux attributs et plus, c’est-à-dire que l’élève a besoin d’au moins une autre habileté pour répondre correctement aux items ;
Le profil 11000 correspond aux élèves qui ne maîtrisent que A1 Repérer des informations explicites et A2 Compréhension globale. Cette combinaison est assez rare, car la compréhension globale fait partie de la compréhension des informations implicites et, dans notre matrice Q, elle est souvent en lien avec A4 Faire des inférences ou A3 Interpréter. Il est donc peu probable que l’élève maîtrise la compréhension globale, mais pas l’interprétation, et qu’il ne puisse pas non plus faire des inférences ;
Le profil 01001, qui fait référence à l’élève qui maîtrise A2 Compréhension globale et A5 Vocabulaire et syntaxe, est peu présent parce que l’attribut A5 Vocabulaire et syntaxe est souvent nécessaire pour répondre aux questions sur l’interprétation et pour faire des inférences, mais il est moins sollicité pour la compréhension globale ;
Le profil 11010 est celui pour lequel les élèves maîtrisent A1 Repérer des informations explicites, A2 Compréhension globale et A4 Faire des inférences, mais pas A3 Interpréter ni A5 Vocabulaire et syntaxe. Cela est peu probable, car l’interprétation est toujours liée à une des quatre autres habiletés, ce qui fait qu’il est rare de maîtriser les trois autres habiletés sans maîtriser l’habileté Interpréter.
Si nous faisons référence aux modèles théoriques en lecture, nous constatons que les modèles interactifs sur lesquels le cadre de référence du test du PIRLS s’appuie mettent en lumière cette nature de complémentarité des habiletés en lecture.
Limites
La première limite de cette recherche émane du fait que l’élaboration de la matrice Q a été réalisée seulement avec le panel d’experts. Nous n’avons pas eu le moyen de vérifier ces attributs identifiés avec les protocoles verbaux des élèves. L’identification des attributs basée principalement sur les propositions des experts et sur le cadre de référence du test du PIRLS 2011 pourrait engendrer le problème de la surspécification des habiletés, car les processus cognitifs pourraient être différents de ce qui s’est passé dans la tête des élèves lors du test. Dans ce cas, les techniques de raffinement de la matrice Q, telles que l’utilisation du test de Wald ou la méthode empirique proposée par de la Torre (2009), sont recommandées pour détecter les problèmes de la sous-spécification ou de la surspécification des attributs. Cela constituerait également une piste importante dans les recherches futures afin d’améliorer l’ajustement des modèles aux données et la qualité diagnostique des items du test du PIRLS.
La seconde limite renvoie au fait que la discussion sur la qualité diagnostique des items du test du PIRLS s’appuie sur les recherches en mathématiques ou en lecture réalisées avec d’autres tests, car il n’existe pas encore de recherches réalisées avec le PIRLS dans une même perspective.
Conclusion
Malgré la qualité diagnostique moyenne des items, ce qui est justifié par le fait que le test n’a pas été initialement conçu à visée diagnostique, les résultats des modélisations montrent bien la possibilité de recevoir des informations plus détaillées sur les forces et les faiblesses cognitives des élèves à travers le test du PIRLS. En effet, le fait que les habiletés sont maîtrisées en gros autour de 50 % est un argument en faveur du potentiel diagnostique du test. D’ailleurs, les résultats suggèrent que les deux modèles (DINA et G-DINA) s’ajustent adéquatement aux données avec les deux matrices Q. Le fait qu’ils s’ajustent mieux avec la matrice Q2_finale que Q1 souligne la nature multidimensionnelle et de complémentarité des habiletés en lecture.
Des recherches dans la même perspective devront se pencher sur le raffinement de la matrice Q, ce qui permettrait d’améliorer la qualité diagnostique des items du test du PIRLS. Les profils détaillés sur la maîtrise ou non des habiletés des élèves avec des pistes d’intervention appropriées pourraient faire l’objet de l’élaboration et de l’évaluation des rapports diagnostiques destinés aux enseignants. Afin d’assurer l’exactitude des profils obtenus, des profils types d’élèves devraient être prévalidés auprès des enseignants avant de procéder à l’élaboration et à l’évaluation en grand nombre des rapports diagnostiques.
Notre recherche a donc montré la faisabilité des modélisations à visée diagnostique des données des épreuves internationales à grande échelle comme le test du PIRLS 2011 avec le DINA et le G-DINA. Cette recherche pourrait donc se transférer dans le contexte des épreuves nationales ou provinciales à grande échelle au primaire, ce qui contribuerait à établir le pont entre les résultats de ces épreuves et l’ADC, visant ultimement à soutenir des élèves en difficulté en lecture.
Parties annexes
Références
- Adams, M. J., & Collins, A. M. (1979). A schema-theoretic view of reading. In R. O. Fredolle (Ed.), Discourse processing : Multidisciplinary Perspectives (pp. 1-22). Norwood, NJ : Ablex.
- Afflerbach, P., & Cho, B. (2009). Identifying and describing constructively responsive comprehension strategies in new and traditional forms of reading. In S. E. Israel & G. G. Duffy (Eds.), Handbook of research on reading comprehension (pp. 69-90). New York, NY : Routledge.
- Alderson, J. C. (2005). Assessing reading. Stutgart, Denmark : Ernst Klett Sprachen.
- Alderson, J. C. (2010). “Cognitive diagnosis and Q-matrices in language assessment” : A commentary. Language Assessment Quarterly, 7(2), 96-103. doi : 10.1080/15434300903426748
- Alderson, J. C., Percsich, R., & Szabo, G. (2000). Sequencing as an item type. Language Testing, 17(4), 423-447. doi : 10.1177/026553220001700403
- Alexander, P. A., & Jetton, T. L. (2000). Learning from text : A multidimensional and developmental perspective. Handbook of reading research, 3, 285-310. doi : 10.4324/9781410605023.ch19
- An, S. (2013). Schema theory in reading. Theory and Practice in Language Studies, 3(1), 130-134. doi : 10.4304/tpls.3.1.130-134
- Anderson, R. C., & Pearson, P. D. (1984). A schema-theoretic view of basic processes in reading comprehension. In P. D. Pearson (Ed.), Handbook of reading research (vol. 1, pp. 255-291). New York, NY : Longman.
- Arican, M., & Sen, S. (2015). A diagnostic comparison of Turkish and Korean students’ mathematics performances on the TIMSS 2011 assessment. Eğitimde ve Psikolojide Ölçme ve Değerlendirme Dergisi/Journal of Measurement and Evaluation in Education and Psychology, 6(2), 238-253. doi : 10.13140/RG.2.1.1262.5362
- Basokcu, T. O. (2014). Classification accuracy effects of Q-matrix validation and sample size in DINA and G-DINA models. Journal of Education and Practice, 5(6), 220-230. Retrieved from https://www.iiste.org/Journals/index.php/JEP/article/view/11253/11543
- Buck, G., & Tatsuoka, K. (1998). Application of the rule-space procedure to language testing : Examining attributes of a free response listening test. Language Testing, 15(2), 119-157. doi : 10.1177/026553229801500201
- Buck, G., Tatsuoka, K., & Kostin, I. (1997). The subskills of reading : Rule-space analysis of a multiple-choice test of second language reading comprehension. Language Learning, 47(3), 423-466. doi : 10.1111/0023-8333.00016
- Carrell, P. L. (1983). Some issues in studying the role of schemata, or background knowledge, in second language comprehension. Reading in a Foreign Language, 1(2), 81-92. Retrieved from http://nflrc.hawaii.edu/rfl/PastIssues/rfl12carrell.pdf
- Carrell, P. L., Devine, J., & Eskey, D. E. (Eds.). (1988). Interactive approaches to second language reading. Cambridge, UK : Cambridge University Press.
- Chen, J., de la Torre, J., & Zhang, Z. (2013). Relative and absolute fit evaluation in cognitive diagnosis modeling. Journal of Educational Measurement, 50(2), 123-140. doi : 10.1111/j.1745-3984.2012.00185.x
- Clay, M. M. (1991). Becoming literate : The construction of inner control. Portsmouth, NH : Heinemann.
- Cui, Y., Gierl, M. J., & Chang, H.-H. (2012). Estimating classification consistency and accuracy for cognitive diagnostic assessment. Journal of Educational Measurement, 49(1), 19-38. doi : 10.1111/j.1745-3984.2011.00158.x
- de la Torre, J. (2009). A cognitive diagnosis model for cognitively based multiple-choice options. Applied Psychological Measurement, 33(3), 163-183. doi : 10.1177/0146621608320523
- de la Torre, J. (2011). The generalized DINA model framework. Psychometrika, 76(2), 179-199. doi : 10.1007/s11336-011-9214-8
- de la Torre, J., & Douglas, J. A. (2008). Model evaluation and multiple strategies in cognitive diagnosis : An analysis of fraction subtraction data. Psychometrika, 73(4), 595-624. doi : 10.1007/s11336-008-9063-2
- Desrosiers, H. et Tétreault, K. (2012). Les facteurs liés à la réussite aux épreuves obligatoires de français en sixième année du primaire : un tour d’horizon. Québec, QC : Institut de la statistique du Québec. Repéré à http://www.stat.gouv.qc.ca/statistiques/education/prescolaire-primaire/reussite-epreuve-francais.html.
- DiBello, L. V., Roussos, L. A., & Stout, W. (2007). Review of cognitively diagnostic assessment and a summary of psychometric models. In C. V. Rao & S. Sinharay (Eds.), Handbook of statistics (pp. 979-1027). Amsterdam, Netherlands : Elsevier.
- Dogan, E., & Tatsuoka, K. (2008). An international comparison using a diagnostic testing model : Turkish students’ profile of mathematical skills on TIMSS-R. Educational Studies in Mathematics, 68(3), 263-272. doi : 10.1007/s10649-007-9099-8
- Dubin, F., Eskey, D. E., Grabe, W., & Savignon, S. (1986). Teaching second language reading for academic purposes. Reading, MA : Addison-Wesley.
- Evran, D. (2019). An application of cognitive diagnosis modeling in TIMSS : A comparison of intuitive definitions of Q-Matrices. International Journal of Modern Education Studies, 3(1), 4-17. Retrieved from https://www.ijonmes.net/index.php/ijonmes/article/view/33
- Fleiss, J. L. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76(5), 378-382. doi : 10.1037/h0031619
- Freedle, R., & Kostin, I. (1993). The prediction of TOEFL reading item difficulty : Implications for construct validity. Language Testing, 10(2), 134-169. doi : 10.1177/026553229301000203
- Gao, L. (2006). Toward a cognitive processing model of MELAB reading test item performance. In J. S. Johnson (Ed.), Spaan fellow working papers in second or foreign language assessment (vol. 4, pp. 1-39). Ann Arbor, MI : University of Michigan. Retrieved from https://www.researchgate.net/profile/Shudong_Wang4/publication/251842392_Validation_and_Invariance_of_Factor_Structure_of_the_ECPE_and_MELAB_across_Gender/links/0f31753889dcc4ef54000000/Validation-and-Invariance-of-Factor-Structure-of-the-ECPE-and-MELAB-across-Gender.pdf
- García, G. (1991). Factors influencing the English reading test performance of Spanish-speaking Hispanic children. Reading Research Quarterly, 26(4), 371-392. doi : 10.2307/747894
- Giasson, J. (1996). La compréhension en lecture. Bruxelles, Belgique : De Boeck Supérieur.
- Gierl, M. J., Cui, Y., & Hunka, S. (2008). Using connectionist models to evaluate examinees’ response patterns to achievement tests. Journal of Modern Applied Statistical Methods, 7(1), 234-245. doi : 10.22237/jmasm/1209615480
- Grabe, W. (1991). Current developments in second language reading research. TESOL Quarterly, 25(3), 375-406. doi : 10.2307/3586977
- Grabe, W. (2000). Reading research and its implications for reading assessment. In A. J. Kunnan (Ed.), Fairness and validation in language assessment (pp. 226-262). Cambridge, UK : Cambridge University Press.
- Hartz, S. M. (2002). A Bayesian framework for the unified model for assessing cognitive abilities : Blending theory with practicality (Unpublished doctoral dissertation). University of Illinois Urbana-Champaign, Champaign, IL.
- Huang, H. Y., & Wang, W. C. (2014). The random‐effect DINA model. Journal of Educational Measurement, 51(1), 75-97. doi : 10.1111/jedm.12035
- Im, S., & Park, H. J. (2010). A comparison of US and Korean students’ mathematics skills using a cognitive diagnostic testing method : Linkage to instruction. Educational Research and Evaluation, 16(3), 287-301. doi : 10.1080/13803611.2010.523294
- Irwin, J. W. (1991). Teaching reading comprehension processes. Englewood, NJ : Prentice-Hall.
- Jang, E. E. (2005). A validity narrative : Effects of reading skills diagnosis on teaching and learning in the context of NG TOEFL (Unpublished doctoral dissertation). University of Illinois Urbana-Champaign, Champaign, IL.
- Jang, E. E. (2009). Cognitive diagnostic assessment of L2 reading comprehension ability : Validity argument for fusion model application to LanguEdge assessment. Language Testing, 26(1), 31-73. doi : 10.1177/0265532208097336
- Junker, B. W., & Sijtsma, K. (2001). Cognitive assessment models with few assumptions, and connections with nonparametric item response theory. Applied Psychological Measurement, 25(3), 258-272. doi : 10.1177/01466210122032064
- Kasai, M. (1997). Application of the rule-space model to the reading comprehension section of the Test of English as a Foreign Language (TOEFL) (Unpublished doctoral dissertation). University of Illinois Urbana-Champaign, Champaign, IL.
- Kintsch, W. (1988). The role of knowledge in discourse comprehension : A construction-integration model. Psychological Review, 95(2), 163-182. doi : 10.1037/0033-295X.95.2.163
- Labrecque, M., Chuy, M., Brochu, P. et Houme, K. (2012). PIRLS 2011 : le contexte au Canada. Toronto, ON : CMEC.
- Langer, J. A. (1990). The process of understanding : Reading for literary and informative purposes. Research in the Teaching of English, 24(3), 229-260. Retrieved from http://www.jstor.org/stable/40171165.
- Lee, Y.-S., Johnson, M., Park, J. Y., Sachdeva, R., Zhang, J., & Waldman, M. (2013, April). A multidimensional scaling (MDS) approach for investigating students’ cognitive weakness and strength on the TIMSS 2007 mathematics assessment. Paper presented at the 2013 Annual Conference of the American Educational Research Association, San Francisco, CA. Retrieved from https://www.researchgate.net/publication/244988418_A_MDS_Approach_for_Investigating_Student’s_Cognitive_Weakness_and_Strength_on_the_TIMSS_2007_Mathematics_Assessment
- Lee, Y.-S., Park, Y. S., & Taylan, D. (2011). A cognitive diagnostic modeling of attribute mastery in Massachusetts, Minnesota, and the U.S. national sample using the TIMSS 2007. International Journal of Testing, 11(2), 144-177. doi : 10.1080/15305058.2010.534571
- Lee, Y.-W., & Sawaki, Y. (2009). Cognitive diagnosis approaches to language assessment : An overview. Language Assessment Quarterly, 6(3), 172-189. doi : 10.1080/15434300902985108
- Lee, Y.-W, & Sawaki, Y. (2011). Application of three cognitive diagnosis models to ESL reading and listening assessments. Language Assessment Quarterly, 6(3), 239-263. doi : 10.1080/15434300903079562
- Leighton, J. P., & Gierl, M. J. (2007). Defining and evaluating models of cognition used in educational measurement to make inferences about examinees’ thinking processes. Educational Measurement : Issues and Practice, 26(2), 3-16. doi : 10.1111/j.1745-3992.2007.00090.x
- Li, H. (2011). A cognitive diagnostic analysis of the MELAB reading test. In J. S. Johnson (Ed.), Spaan fellow working papers in second or foreign language assessment (vol. 9, pp. 17-46). Ann Arbor, MI : University of Michigan. Retrieved from https://www.academia.edu/9788619/A_cognitive_diagnostic_analysis_of_the_MELAB_reading_test
- Li, H., & Suen, H. K. (2013). Constructing and validating a Q-matrix for cognitive diagnostic analyses of a reading test. Educational Assessment, 18(1), 1-25. doi : 10.1080/10627197.2013.761522
- Loye, N. (2010). 2010, odyssée des modèles de classification diagnostique (MCD). Mesure et évaluation en éducation, 33(3), 75-98. doi : 10.7202/1024892ar
- Loye, N. et Lambert-Chan, J. (2016). Au coeur du développement d’une épreuve en mathématique dotée d’un potentiel diagnostique. Mesure et évaluation en éducation, 39(3), 29-57. doi : 10.7202/1040136ar
- Ma, W., Iaconangelo, C., & de la Torre, J. (2016). Model similarity, model selection, and attribute classification. Applied Psychological Measurement, 40(3), 1-18. doi : 10.1177/0146621615621717
- Ma, X., & Meng, Y. (2014). Towards personalized English learning diagnosis : Cognitive diagnostic modelling for EFL listening. Asian Journal of Education and e-Learning, 2(5), 336-348. Retrieved from https://ajouronline.com/index.php/AJEEL/article/view/1669
- Mullis, I. V., Martin, M. O., Kennedy, A. M., Trong, K. L., & Sainsbury, M. (2009). PIRLS 2011 assessment framework. Amsterdam, Netherlands : International Association for the Evaluation of Educational Achievement.
- Pagani, L. S., Fitzpatrick, C., Belleau, L. et Janosz, M. (2011). Prédire la réussite scolaire des enfants en quatrième année à partir de leurs habiletés cognitives, comportementales et motrices à la maternelle. Étude longitudinale du développement des enfants du Québec (ÉLDEQ 1998-2010) : de la naissance à 10 ans. Repéré àhttp://www.jesuisjeserai.stat.gouv.qc.ca/publications/fascicule_reussite_scol_fr.pdf
- Ravand, H., Barati, H., & Widhiarso, W. (2013). Exploring diagnostic capacity of a high stakes reading comprehension test : A pedagogical demonstration. Iranian Journal of Language Testing, 3(1), 11-37. Retrieved from https://www.researchgate.net/publication/281558416_Exploring_Diagnostic_Capacity_of_a_High_Stakes_Reading_Comprehension_Test_A_Pedagogical_Demonstration
- Rumelhart, D. E. (1978). Schemata : The building blocks of cognition. San Diego, CA : Center for Human Information Processing, University of California.
- Rupp, A., Templin, J., & Henson, R. A. (2010). Diagnostic measurement : Theory, methods, and applications. New York, NY : Guilford Press.
- Samuels, S. J., & Kamil, M. L. (1984). 7 Models of the reading process. In P. D. Pearson (Ed.), Handbook of reading research (pp. 185-224). Mahwah, NJ : Lawrence Erlbaum.
- Scott, H. S. (1998). Cognitive diagnostic perspectives of a second language reading test (Unpublished doctoral dissertation). University of Illinois Urbana-Champaign, Champaign, IL.
- Sinharay, S. (2004). Experiences with Markov chain Monte Carlo convergence assessment in two psychometric examples. Journal of Educational and Behavioral Statistics, 29(4), 461-488. doi : 10.3102/10769986029004461
- Snow, C. (2002). Reading for understanding : Towards an R&D program in reading comprehension. Santa Monica, CA : Rand.
- Stanovich, K. E. (1980). Toward an interactive-compensatory model of individual differences in the development of reading fluency. Reading Research Quarterly, 16(1), 32-71. doi : 10.2307/747348
- Templin, J., & Henson, R. A. (2006). Measurement of psychological disorders using cognitive diagnosis models. Psychological Methods, 11(3), 287-305. doi : 10.1037/1082-989X.11.3.287
- Terzi, R., & Sen, S. (2019). A nondiagnostic assessment for diagnostic purposes : Q-matrix validation and item-based model fit evaluation for the TIMSS 2011 assessment. SAGE Open, 9(1), 1-11. doi : 10.1177/2158244019832684
- Tjoe, H., & de la Torre, J. (2014). The identification and validation process of proportional reasoning attributes : An application of a cognitive diagnosis modeling framework. Mathematics Educational Research Journal, 26(2), 237-255. doi : 10.1007/s13394-013-0090-7
- Toker, T., & Green, K. (2012, April). An application of cognitive diagnostic assessment on TIMMS-2007 8th grade mathematics items. Paper presented at the Annual Meeting of the American Educational Research Association, Vancouver, BC. Retrieved from https://files.eric.ed.gov/fulltext/ED543803.pdf
- van Dijk, T. A., & Kintsch, W. (1983). Strategies of discourse comprehension. New York, NY : Academic Press.
- von Davier, M. (2008). A general diagnostic model applied to language testing data. Princeton, NJ : ETS.
- Wafa, M. N. (2019). Assessing school students’ mathematic ability using DINA and DINO models. International Journal of Mathematics Trends and Technology (IJMTT), 65(12), 153-165. Retrieved from http://www.ijmttjournal.org/Volume-65/Issue-12/IJMTT-V65I12P517.pdf
- Wafa, M. N., Hussaini, S. A. M., & Pazhman, J. (2020). Evaluation of students’ mathematical ability in Afghanistan’s schools using cognitive diagnosis models. Eurasia Journal of Mathematics, Science and Technology Education, 16(6), em1849. doi : 10.29333/ejmste/7834
- Yamaguchi K., & Okada, K. (2018). Comparison among cognitive diagnostic models for the TIMSS 2007 fourth grade mathematics assessment. PLOS ONE, 13(2), e0188691. doi : 10.1371/journal.pone.0188691
- Yang, X., & Embretson, S. E. (2007). Construct validity and cognitive diagnostic assessment. In J. P. Leighton & M. J. Gierl (Eds.), Cognitive diagnostic assessment for education : Theory and applications (pp. 119-145). Cambridge, UK : Cambridge University Press. Retrieved from https://pdfs.semanticscholar.org/32a5/00670eced66b3023e45a8b0929ad4c1f46e3.pdf
Liste des figures
Figure 1
Estimation des paramètres d’items et leur qualité diagnostique
Figure 2.
Probabilités de maîtrise des attributs pour l’ensemble des élèves
Liste des tableaux
Tableau 1
Description des processus et répartition des items
Tableau 2
Probabilités de réponse dans le modèle DINA (adapté de Rupp, Templin et Henson, 2010)
Tableau 3
Matrice Q1 élaborée à partir du cadre de référence du test du PIRLS 2011
Tableau 4
Définitions détaillées des attributs
Tableau 5
Matrice Q2 initiale élaborée par les experts
Tableau 6
Répartition des items selon le taux de concordance des experts
Tableau 7
Matrice Q2_finale proposée pour des modélisations du test du PIRLS 2011
Tableau 8
Ajustement relatif des modèles aux données avec les matrices Q1 et Q2_finale
Tableau 9
Ajustement absolu des modèles aux données avec les matrices Q1 et Q2_finale
Tableau 10
Estimation des paramètres d’items avec la matrice Q2_finale et avec DINA
Tableau 11
Profils et pourcentages des participants