Abstracts
Résumé
Cet article brosse le portrait des écarts d’anxiété mathématique selon le genre et du lien anxiété mathématique/performances en mathématiques chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012. Après avoir vérifié l’invariance métrique et scalaire de la mesure d’anxiété mathématique du PISA, entre les garçons et les filles, les résultats de cet article révèlent qu’en moyenne, les filles francophones de 15 ans du Québec font état d’un niveau d’anxiété mathématique statistiquement plus élevé que les garçons. En outre, les résultats de 2003 et de 2012 montrent que le lien négatif anxiété mathématique/performances en mathématiques est équivalent chez les garçons et chez les filles et donc, qu’il ne semble pas y avoir d’effet de modération de ce lien, par le genre. De là, l’article se penche sur les stratégies d’intervention qui pourraient permettre de réduire l’importance du lien négatif anxiété mathématique/performances en mathématiques, chez les personnes qui se disent anxieuses à l’égard des mathématiques.
Mots-clés :
- anxiété mathématique,
- évaluations à grande échelle en éducation,
- évaluations internationales en éducation,
- facteurs de réussite en mathématiques,
- performances en mathématiques,
- PISA
Abstract
This article paints a portrait of the differences in mathematical anxiety according to gender and the link between mathematical anxiety and mathematical performance, among 15-year-old French-speaking Quebec students who participated in PISA in 2003 and 2012. After verifying the metric and scalar invariance of the PISA mathematical anxiety measure, between boys and girls, the results of this article reveal that, on average, 15-year-old French-speaking girls in Quebec report a statistically higher level of mathematical anxiety than boys. In addition, the results of 2003 and 2012 show that the negative link between mathematical anxiety and mathematical performance is equivalent in boys and girls and, therefore, there does not seem to be any moderating effect on this link, by gender. From there, the article focuses on the intervention strategies that could reduce the importance of the negative link between mathematical anxiety and mathematical performance, in individuals who claim to be anxious about mathematics.
Keywords:
- large-scale educational assessments,
- mathematics anxiety,
- mathematics performance,
- PISA,
- success factors in mathematics
Resumo
Este artigo descreve as disparidades de ansiedade matemática por género e a relação entre ansiedade matemática e desempenho em matemática entre alunos francófonos do Quebec de 15 anos que participaram do PISA em 2003 e 2012. Após verificar a invariância métrica e escalar da medida de ansiedade matemática do PISA, entre os rapazes e as raparigas, os resultados deste artigo revelam que, em média, as raparigas francófonas de 15 anos do Quebec relatam um nível de ansiedade matemática estatisticamente mais alto do que os rapazes. Além disso, os resultados de 2003 e 2012 mostram que a relação negativa entre ansiedade matemática/desempenho em matemática é equivalente entre os rapazes e as raparigas, sugerindo, portanto, que não parece haver um efeito moderador do género nessa relação. A partir daí, o artigo investiga estratégias de intervenção que poderiam ajudar a reduzir a importância da relação negativa entre ansiedade matemática/desempenho em matemática entre indivíduos que expressam ansiedade em relação à matemática.
Palavras chaves:
- ansiedade matemática,
- avaliações em grande escala em educação,
- avaliações internacionais em educação,
- fatores de sucesso em matemática,
- desempenhos em matemática,
- PISA
Article body
Problématique
Les mathématiques sont omniprésentes dans notre société, tantôt sous la forme d’habiletés de base, tantôt sous la forme d’outils plus sophistiqués, nichés dans diverses applications en sciences pures et appliquées, en sciences de la santé, en sciences humaines et sociales, en finances, etc. Dans ce contexte, bien performer dans le domaine constitue un atout de taille car de grands enjeux académiques, professionnels, personnels et sociétaux y sont rattachés.
Du point de vue académique, des études longitudinales montrent que les performances en mathématiques sont liées positivement à la probabilité d’obtenir un diplôme d’études secondaire (Chiu & Klassen, 2010 ; Ma, 1999 ; OCDE, 2014a ; Parsons & Bynner, 2005 ; Stokke, 2015), à la probabilité de réussir la transition vers les études supérieures et à la probabilité d’obtenir un diplôme d’études postsecondaires (Chiu & Klassen, 2010 ; Ma, 1999 ; OCDE, 2014a ; Parsons & Bynner, 2005 ; Stokke, 2015). Du point de vue professionnel, des tendances tout aussi similaires s’observent. En effet, les résultats en mathématiques au secondaire et au postsecondaire permettent de prédire le niveau d’employabilité des personnes et même leurs revenus professionnels éventuels (Joensen & Nielsen, 2009 ; Ma, 1999 ; Parsons & Bynner, 2005). À ce sujet, une étude québécoise révèle que « pour les travailleurs actifs de la population québécoise, une augmentation d’un écart type des compétences en numératie[1] est associée à une augmentation de 21 % du salaire » (Fonseca et al., 2021, p. 1).
Il semble en outre, en regard de la sphère de vie personnelle, que les performances en mathématiques sont liées à la capacité à faire des choix de vie éclairés. De ce fait, les performances dans le domaine permettent de prédire la qualité de vie des personnes et même, leur longévité (Geary, 1996 ; Reyna & Brainerd, 2007 ; Rivera-Batiz, 1992). Aussi, comme les personnes plus performantes en mathématiques sont davantage susceptibles de se percevoir comme des « acteurs plutôt que comme des objets des processus politiques » (OCDE, 2014a, p. 268), les performances en mathématiques permettent de prédire la probabilité, pour une personne, de s’engager activement dans son milieu de vie.
Ainsi, collectivement, c’est l’ensemble d’une société qui bénéficie des retombées individuelles positives liées aux bonnes performances en mathématiques. À preuve, plus les performances en mathématiques sont élevées dans une société, plus cette société est susceptible de croître, économiquement (Geary, 1996 ; Moses & Cobb, 2001 ; Peterson et al., 2011).
À l’ensemble de ces enjeux de nature individuelle et collective s’ajoutent deux défis sociétaux importants, spécifiques aux professions liées aux mathématiques, les professions regroupées sous l’acronyme STIM pour sciences, technologie, ingénierie et mathématiques. Le premier concerne la pénurie de main-d’oeuvre qualifiée dans les STIM, depuis le début des années 2000, dans plusieurs pays et nations dont le Québec, le Canada (Pronovost et al., 2017) et les États-Unis (Beilock & Maloney, 2015). Le second a trait à la sous-représentation des femmes dans ces professions (Encinas-Martín & Cherian, 2023 ; Stoet et al., 2016) et ce, même dans les pays les plus développés et les plus sensibles à l’égalité des chances entre les sexes (Stoet et al., 2016). Or, les performances en mathématiques sont reconnues pour expliquer, en partie, ces deux phénomènes (Encinas-Martín & Cherian, 2023). En effet, les personnes plus performantes en mathématiques sont davantage susceptibles de se diriger vers les STIM (Jacobs & Morita, 2002 ; Wang et al., 2013).
Au vu de l’ensemble de ce contexte, un défi colossal s’impose aux sociétés et aux systèmes éducatifs en général : faire en sorte que chaque apprenant performe à la hauteur de son potentiel en mathématiques (OCDE, 2014b). Heureusement, à cet égard, les résultats du TIMSS (Trends in Mathematics and Sciences Study[2]) de 4e année et de 8e année et ceux du PISA (Programme international de l’OCDE pour le suivi des acquis des élèves[3]) montrent que, lors de ces épreuves standardisées, les élèves québécois se classent très bien sur la scène internationale en mathématiques. En effet, aux 20 cycles de ces enquêtes auxquels ils ont participé depuis 1995, les élèves québécois ont obtenu des scores moyens au-dessus de la moyenne internationale (Brochu et al., 2013 ; Bussière et al., 2004 ; Mullis et al., 2004 ; Mullis et al., 2008 ; Mullis et al., 2012 ; Mullis et al., 2016 ; Mullis et al., 2020 ; O’Grady et al., 2016 ; O’Grady et al., 2019). De surcroît, à l’ensemble des épreuves du TIMSS de 8e année depuis 2003, puis à l’ensemble des épreuves du PISA depuis 2000, les élèves québécois se sont classés au sein des 10 pays/économies en tête de peloton (Brochu et al., 2013 ; Bussière et al., 2004 ; Mullis et al., 2004 ; Mullis et al., 2008 ; Mullis et al., 2012 ; Mullis et al., 2016 ; Mullis et al., 2020 ; O’Grady et al., 2016 ; O’Grady et al., 2019).
Des analyses plus fines font toutefois état de constats préoccupants. En effet, à 10 des 20 épreuves auxquelles les élèves québécois ont participé, les filles ont obtenu des résultats statistiquement inférieurs à ceux des garçons (p < 0,05). Qui plus est, aux épreuves du PISA de 2003, de 2012 et de 2018, toute proportion gardée, les filles québécoises ont été moins nombreuses que les garçons à se hisser dans les premiers rangs (Brochu et al., 2013 ; Mullis et al., 2016 ; OCDE, 2014a ; OCDE, 2016 ; O’Grady et al., 2016, 2019). En effet, en 2003, 25,9 % des garçons québécois se sont classés dans les niveaux de compétence les plus élevés de l’échelle de compétence en culture mathématique du PISA, alors que seulement 19,3 % des filles ont atteint ces niveaux. En 2012 et en 2018, ces pourcentages ont été respectivement de 25,3 % pour les garçons contre 19,5 % pour les filles, puis 23,2 % pour les garçons contre 19,0 % pour les filles (p < 0,05 dans les deux cas) (Brochu et al., 2013 ; Bussière et al., 2004 ; O’Grady et al., 2019).
L’anxiété mathématique, un phénomène défini comme « une sensation de tension et d’anxiété qui interfère avec la manipulation des nombres et la résolution de problèmes mathématiques dans une grande diversité de situations de la vie courante et de situations académiques [notre traduction] » (Richardson & Suinn, 1972, p. 551), pourrait contribuer aux différences de performances observées entre les garçons et les filles, en mathématiques (Stoet et al., 2016). En effet, les recherches menées sur le sujet dans divers pays, depuis les années 1970 révèlent que, de manière générale, chez les adolescents et chez les adultes, les filles se disent davantage anxieuses à l’égard des mathématiques que les garçons (Else-Quest et al., 2010 ; Hyde et al., 1990 ; Stoet et al. 2016). De plus, dans ces mêmes groupes d’âge, une corrélation linéaire négative est observée entre le niveau d’anxiété mathématique d’une personne et ses performances en mathématiques (Barroso et al., 2021 ; Hembree, 1990 ; Ma, 1999 ; Zhang et al., 2019).
Comme l’anxiété mathématique est aussi reconnue pour engendrer de l’évitement des mathématiques (Ashcraft, 2002 ; Ashcraft & Moore, 2009 ; Hembree, 1990), il apparaît d’autant plus indiqué de nous intéresser au phénomène, au vu de l’ensemble du contexte évoqué ci-haut. En effet, l’anxiété mathématique est mise en cause pour expliquer, en partie, la pénurie de main-d’oeuvre dans les STIM et la sous-représentation des femmes dans ces domaines (Encinas-Martín & Cherian, 2023 ; Stoet et al., 2016).
En 2003 et en 2012, le PISA s’est intéressé à l’anxiété mathématique. En effet, comme les mathématiques ont constitué le domaine majeur d’évaluation lors de ces deux enquêtes, l’anxiété mathématique a été documentée à ces occasions, au même titre que bon nombre d’autres facteurs non-cognitifs liés aux performances dans le domaine. Pour ce faire, l’OCDE a développé un questionnaire auto-rapporté de l’anxiété mathématique, un instrument de mesure constitué de cinq items allant comme suit : « Je m’inquiète souvent en pensant que j’aurai des difficultés en mathématiques », « Je suis très tendu quand j’ai un devoir de mathématiques à faire », « Je deviens très nerveux quand je travaille à des problèmes de mathématiques », « Je me sens perdu quand j’essaie de résoudre un problème de mathématiques » et, enfin, « Je m’inquiète à l’idée d’avoir de mauvaises notes en mathématiques ». Les participants ont été invités à indiquer dans quelle mesure ils étaient d’accord ou pas avec chacun des énoncés, à l’aide d’une échelle de type Likert en quatre points (1- tout à fait d’accord, 2- d’accord, 3- pas d’accord et 4- pas du tout d’accord) (OCDE, 2014b, p. 206).
Le Canada est l’un des 39 pays/économies à avoir participé à la fois au cycle du PISA de 2003 et à celui de 2012 (OCDE, 2014b, annexe B1, tableau III.4.3d). Les résultats issus de ces enquêtes révèlent qu’en 2003 et en 2012, les filles canadiennes de 15 ans se sont dites davantage anxieuses à l’égard des mathématiques que les garçons canadiens de 15 ans (OCDE, 2005a, 2014b). L’importance de la disparité en matière d’anxiété mathématique observée selon le genre au Canada, en 2012, a même placé le pays au 4e rang sur les 34 pays/économies membres de l’OCDE à avoir participé à l’épreuve (OCDE, 2014b, chap. 4, annexe B1, tableau III.4.3d). Les résultats canadiens de 2003 et de 2012 ont aussi fait état d’une corrélation négative entre le niveau d’anxiété mathématique des élèves canadiens et leurs performances en mathématiques (OCDE, 2005a, chap. 3, annexe B1, tableau 3.8 ; OCDE, 2014b, chap. 4, annexe B1, tableau III.4.3d).
Ce portrait canadien, issu du PISA de 2003 et de 2012, appuie et renforce l’idée selon laquelle l’anxiété mathématique pourrait contribuer à expliquer les écarts de performances observés entre les garçons et les filles, en mathématiques, au Québec. Dans le contexte, il apparaît pertinent de tirer profit des données du PISA, des données publiques, disponibles sur deux cycles, pour quantifier la disparité d’anxiété mathématique selon le genre, chez les élèves québécois, puis pour étudier le lien anxiété mathématique/performances en mathématiques chez ces mêmes élèves. Les résultats obtenus pourront par la suite servir d’assises pour étudier des facteurs permettant d’expliquer les écarts observés et guider éventuellement la mise en oeuvre d’interventions efficaces en vue de les réduire.
Toutefois, comme les élèves québécois ayant participé au PISA de 2003 et de 2012 se subdivisent en deux sous-groupes (les élèves issus du système scolaire francophone et les élèves issus du système scolaire anglophone), nous avons fait le choix de nous concentrer, dans cette recherche, sur le sous-groupe d’élèves majoritaire au Québec, à savoir les élèves issus du système scolaire francophone. Cette décision a été prise à la suite d’analyses préalables confirmant, dans ce sous-groupe, la présence des mêmes écarts de performance selon le genre que ceux révélés pour l’ensemble des élèves québécois ayant participé au PISA de 2003 et de 2012.
Dès lors, nous utiliserons l’expression « élèves québécois francophones » afin de désigner les élèves québécois issus d’écoles du système scolaire francophone. De ce fait, nous énonçons l’objectif général de notre recherche comme suit : quantifier les écarts d’anxiété mathématique selon le genre et étudier le lien anxiété mathématique/performances en mathématiques chez les élèves québécois francophones de 15 ans, à partir d’une analyse secondaire des données du PISA de 2003 et de 2012.
Cadre théorique
Un bref historique de la recherche sur le concept d’anxiété mathématique
Selon Ashcraft et Ridley (2005), Gough (1954) aurait été la première à émettre l’hypothèse que les mathématiques puissent déclencher, chez certains apprenants, une forme d’anxiété particulière, susceptible de nuire aux apprentissages et aux performances dans le domaine. En effet, en cherchant à comprendre pourquoi certaines personnes très performantes académiquement parvenaient difficilement à réussir en mathématiques (Suárez-Pellicioni et al., 2016), Gough aurait proposé le concept de mathémaphobie.
Le concept d’anxiété mathématique, quant à lui, a été introduit officiellement par Richardson et Suinn en 1972 au moment de soumettre le premier instrument de mesure formel du phénomène, le MARS (Mathematics Anxiety Rating Scale). À la suite de la publication du MARS, une panoplie d’autres instruments de mesure de l’anxiété mathématique ont vu le jour : le sMARS (25-items shortened Mathematics Anxiety Rating Scale) de Alexander et Martray (1989), le MAS (12-items Mathematics Anxiety Scale) de Fennema-Sherman (1976), l’ATMS (6-items Anxiety Towards Mathematics Scale) de Sandman (1980), le AMAS (9-items Abbreviated Math Anxiety Scale) de Hopko et al. (2003) ou encore le MARS30-Brief scale de Pletzer et al. (2016). Alors que ces instruments ont été développés pour appréhender le phénomène principalement chez les adolescents et chez les adultes, le MAAQ (Mathematics Attitude and Anxiety Questionnaire) (Dowker et al., 2012 ; Thomas & Dowker, 2000), pour sa part, a été développé pour un usage particulier, auprès des enfants.
Malgré le vaste inventaire d’outils permettant d’appréhender le niveau d’anxiété mathématique ressenti par les personnes, le MARS, doté de bonnes qualités psychométriques avec une consistance interne α = 0,97 et une fidélité test-retest sur deux semaines de 0,85 (Richardson & Suinn, 1972) est demeuré l’instrument de mesure de prédilection, à tout le moins jusqu’à la fin des années 1990. C’est d’ailleurs à partir d’un corpus de recherches entièrement menées à l’aide du MARS qu’Hembree (1990) a pu fournir la première méta-analyse sur le sujet de l’anxiété mathématique, un article phare dans le domaine.
Après avoir répertorié 151 études publiées entre 1970 et 1990, Hembree (1990) s’est d’abord vu en mesure de fournir les premiers éléments permettant de distinguer l’anxiété mathématique d’autres formes d’anxiété comme l’anxiété d’évaluation (Alpert & Haber, 1960, cité dans Hembree, 1990), la prédisposition générale à l’anxiété (general anxiety proneness) (Spielberger, 1972, cité dans Hembree, 1990, p. 40) ou encore les deux composantes de la prédisposition générale à l’anxiété : le trait d’anxiété chronique (chronic A-trait) et l’état anxieux transitoire (transitory A-state) (Spielberger, 1972, cité dans Hembree, 1990, p. 40). À partir des corrélations obtenues entre chacun de ces concepts et l’anxiété mathématique, soit des valeurs respectives de r = 0,52, r = 0,35, r = 0,38 et r = 0,42, Hembree (1990) a proposé de traiter l’anxiété mathématique comme un concept à part entière, une conclusion largement citée dans les écrits subséquents sur l’anxiété mathématique.
Grâce à sa méta-analyse, Hembree (1990) a également pu mettre en exergue l’importance académique du phénomène. En effet, ses résultats ont levé le voile sur le lien linéaire négatif entre l’anxiété mathématique et les performances dans le domaine (r = -0,30 chez les élèves de la 9e à la 12e année), puis sur l’association positive entre l’anxiété mathématique et l’évitement des cours de mathématiques (r = -0,31 entre le niveau d’anxiété mathématique et le nombre de cours de mathématiques suivis au secondaire).
À la suite d’Hembree (1990), des chercheurs comme Ma, Faust, Ashcraft, Lyons, Beilock, Maloney, Ramirez, leurs collaborateurs et bien d’autres encore, se sont aussi intéressés à l’anxiété mathématique. À partir de 26 études publiées entre 1970 et 1999, Ma (1999) a réalisé une méta-analyse faisant état d’une corrélation de -0,3 entre l’anxiété mathématique et les performances chez des élèves de la 4e à la 12e année, corroborant ainsi les résultats révélés par Hembree (1990) chez les élèves de la 9e à la 12e année.
Pour leur part, Faust (1992) et Lyons et Beilock (2012) se sont intéressés, notamment, aux signes et aux symptômes de l’anxiété mathématique. Faust (1992) a montré qu’en plus de s’accompagner de ruminations et de pensées négatives, l’anxiété mathématique peut se caractériser par la présence de sudation abondante, de tremblements, d’étourdissements, de nausée, de douleur abdominale, couplés à une augmentation du rythme cardiaque. Grâce à la neuro-imagerie fonctionnelle, Lyons et Beilock (2012) ont montré que la simple anticipation d’une tâche mathématique peut, chez les personnes qui se disent anxieuses à l’égard des mathématiques, déclencher une augmentation de l’activité dans une des zones cérébrales impliquées dans la perception de la douleur (le cortex insulaire dorso-postérieur). Ainsi, pour ces individus, « […] le simple fait de savoir qu’ils vont se retrouver devant un problème mathématique peut être douloureux » (OCDE, 2014b, p. 100). De ce fait, pour ces personnes, éviter les mathématiques devient aussi naturel que de chercher à éviter une douleur (OCDE, 2014b).
Les travaux menés par Ashcraft et Kirk (2001), par Maloney (2016), par Maloney et al. (2010, 2011, 2012) par Ferguson et al. (2015) et par Ramirez et al. (2018) ont fourni trois hypothèses permettant d’expliquer le lien négatif entre l’anxiété mathématique et les performances en mathématiques. La première, l’hypothèse dite de l’interférence (disruption account) (Ramirez et al., 2018), stipule que les ruminations et les pensées négatives qui accompagnent l’anxiété mathématique (la cause) nuiraient aux performances en mathématiques (la conséquence) en consommant une partie des ressources cognitives limitées (Ashcraft & Kirk, 2001). La seconde, l’hypothèse dite du déficit (reduced competency account) (Ramirez et al., 2018), stipule qu’un déficit au niveau de certaines habiletés de base en mathématiques (l’habileté à dénombrer des objets, l’habileté à ordonner des nombres et l’habileté spatiale) entraînerait de moins bonnes performances en mathématiques (Ferguson et al., 2015 ; Maloney, 2016 ; Maloney et al., 2010 ; Maloney et al., 2011 ; Maloney et al., 2012). Ces moins bonnes performances en mathématiques (la cause) engendreraient de l’anxiété mathématique (la conséquence). La troisième hypothèse, celle de l’interprétation (interpretation account) (Ramirez et al., 2018), propose l’idée que l’anxiété mathématique découle de l’interprétation que font les personnes de leurs expériences présentes et passées en mathématiques et de leurs résultats. Une fois déclenchée, l’anxiété mathématique et les faibles performances en mathématiques se nourrissent les unes et les autres.
Encore aujourd’hui, la structure factorielle du concept d’anxiété mathématique reste incertaine (Cipora et al., 2019). En effet, bien que la plupart des chercheurs s’entendent pour dire que l’anxiété mathématique n’est pas un concept unidimensionnel, pour certains, il s’agit d’un concept composé de deux, trois ou même six facteurs, alors que d’autres proposent une structure hiérarchique (Cipora et al., 2019). Pour Suinn et Edwards (1982) et pour Hopko et al. (2003), l’anxiété mathématique, telle qu’appréhendée par le MARS et le AMAS respectivement, comprend deux facteurs : l’anxiété liée à l’utilisation des mathématiques dans la vie de tous les jours, appelée l’anxiété numérique (numerical anxiety) et l’anxiété d’évaluation en mathématiques, appelée l’anxiété de test en mathématiques (math test anxiety) par Suinn et Edwards (1982). Hopko et al (2003) ont quant à eux nommé ces formes d’anxiété l’anxiété d’apprentissage en mathématiques (learning math anxiety) et l’anxiété d’évaluation en mathématiques (math evaluation anxiety). Pour Alexander et Martray (1989), une structure à trois facteurs explique mieux qu’une structure à deux facteurs la variance de l’anxiété mathématique telle qu’appréhendée par le sMARS. Ces trois facteurs sont l’anxiété de test en mathématiques (math test anxiety), l’anxiété liée à une tâche numérique (numerical task anxiety) et l’anxiété liée aux cours de mathématiques (math course anxiety) respectivement, (Cipora et al., 2019, p. 21). Pour Pletzer et al. (2016), une structure à six facteurs est celle qui explique le mieux la variance de l’anxiété mathématique telle qu’appréhendée par le MARS30-Brief scale (Pletzer et al., 2016).
Enfin, alors que les structures proposées ci-haut découlent de situations et de contextes dans lesquels l’anxiété mathématique est ressentie, Ho et al. (2000) proposent une structure faisant abstraction de la situation et du contexte. Pour ces auteurs, l’anxiété mathématique est un concept à deux composantes : la composante affective (sensation de tension, appréhension, etc.) et la composante cognitive (ruminations et pensées négatives).
Les écarts d’anxiété mathématique selon le genre et le lien anxiété mathématique/performances selon le genre
Un certain nombre de recherches menées depuis les années 1990 se sont intéressées aux écarts d’anxiété mathématique moyens, selon le genre. La vaste majorité des recherches menées en ce sens auprès de populations adolescentes ou auprès de populations adultes ont montré que, de manière générale, les filles se disent davantage anxieuses à l’égard des mathématiques que les garçons. Parmi ces recherches figurent la méta-analyse d’Hembree (1990), de même que celles d’Hyde et al. (1990) et de Else-Quest et al. (2010). Hembree a fait état d’écarts dans le niveau moyen d’anxiété mathématique des garçons et des filles, dont la taille d’effet s’est élevée à 0,19, chez les élèves de la 5e à la 12e année, puis à 0,31, chez les étudiants de niveau postsecondaire.
À partir de 70 études publiées entre 1967 et 1988, Hyde et al. (1990) ont aussi fait état d’écarts dans le niveau moyen d’anxiété mathématique des filles et des garçons de 11 à 25 ans. La taille d’effet, (calculée de la manière suggérée par Hedges et Becker, 1986, cités dans Hyde et al., 1990, p. 305) s’est élevée à 0,16. Enfin, la méta-analyse d’Else-Quest et al. (2010), effectuée à partir d’une analyse secondaire des données internationales du PISA de 2003 et du TIMSS 8e année de 2003 (493 495 élèves âgés de 14 à 16 ans), a révélé une différence dans le niveau moyen d’anxiété mathématique des filles et des garçons, avec une taille d’effet calculée à la manière de Hedges et Becker (1986), cité dans Else Quest et al. (2010, p. 115) de 0,28. En outre, en regard de la tendance de cet écart, les résultats du PISA révèlent que, dans les pays de l’OCDE, l’écart d’anxiété mathématique selon le genre a augmenté dans une mesure statistiquement significative, entre 2003 et 2012 (OCDE, 2014b).
En ce qui a trait au lien linéaire négatif anxiété mathématique/performances en mathématiques, quatre méta-analyses ont documenté les différences selon le genre : celle d’Hembree (1990), celle de Ma (1999), celle de Zhang et al. (2019) et celle de Barroso et al. (2021). La méta-analyse d’Hembree (1990) a fait état d’un lien linéaire négatif anxiété mathématique/performances en mathématiques plus important chez les garçons que chez les filles, chez les élèves de la 5e à la 12e année (r = -0,36 chez les garçons, r = -0,30 chez les filles), mais similaire chez les étudiants du postsecondaire (r = -0,34). La méta-analyse de Ma (1999) a fait état d’un lien linéaire négatif anxiété mathématique/performances similaire, chez les garçons et chez les filles de la 4e à la 12e année (r = -0,30). À partir de 49 études publiées entre 2000 et 2019, Zhang et al. (2019) ont révélé un lien linéaire négatif équivalent chez les garçons et les filles, chez des élèves de niveau primaire et secondaire, puis des étudiants de niveau postsecondaire (r = -0,33). Enfin, à partir de 747 tailles d’effet, Barroso et al. (2021) ont également fait état d’un lien linéaire négatif équivalent chez les garçons et les filles, chez des élèves de niveau primaire et secondaire, puis des étudiants de niveau postsecondaire. Ainsi, contrairement à la méta-analyse d’Hembree (199) qui a révélé un effet modérateur du genre sur le lien anxiété mathématique/performances en mathématiques, celles de Ma (1999), de Zhang et al. (2019) et de Barroso et al. (2021) n’ont pas révélé cet effet modérateur.
Les objectifs spécifiques de recherche
À la lumière de ces résultats, nous définissons les objectifs spécifiques de notre recherche et nos hypothèses de recherche comme suit :
OS1 – Quantifier les écarts d’anxiété mathématique entre les filles et les garçons francophones de 15 ans du Québec ayant participé au PISA de 2003 et de 2012 et documenter la tendance 2003-2012 de ces écarts.
Hypothèse : Les filles québécoises francophones de 15 ans se disent davantage anxieuses à l’égard des mathématiques que les garçons québécois francophones de 15 ans et la tendance 2003-2012 révèle une hausse de l’écart.
OS2 - Vérifier si le lien linéaire anxiété mathématique/performance est négatif et si le genre modère ce lien chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012
Hypothèse : Le lien linéaire anxiété mathématique/performance est négatif et il n’y a pas de modération de ce lien par le genre.
Méthodologie
Les données analysées dans la présente recherche sont des données issues du PISA de 2003 et de 2012. Dans le cadre du PISA, l’OCDE a recours à des techniques d’échantillonnage, de collecte et d’analyse de données particulières. En effet, les échantillons sont d’abord générés, dans chacun des pays participants, au moyen d’un plan d’échantillonnage dit plan d’échantillonnage complexe (complexe sampling design) (Lohr, 2019 ; Rutkovski et al., 2010 ; Skinner & Wakefield, 2017 ; Stapleton, 2013). Plus précisément, l’échantillonnage suit un plan aléatoire stratifié en deux niveaux (des écoles sont sélectionnées au premier niveau et des élèves, nichés à l’intérieur de ces écoles, sont sélectionnés au deuxième niveau). Puis, au moment de la collecte de données, un plan de collecte particulier appelé devis en trois formes (three-form design) (Graham et al., 1996) peut être mis en oeuvre. Un tel plan a en effet été employé, dans le cadre du PISA 2012, au moment de documenter l’anxiété mathématique. Finalement, pour rendre compte du niveau d’habileté en mathématiques, l’OCDE fournit non pas une seule valeur mais plutôt cinq valeurs appelées valeurs plausibles.
Vohl et Loye (sous presse) et Vohl (2023, chap. 3) présentent, dans le détail, ce qui est entendu par plan d’échantillonnage complexe, devis en trois formes et valeurs plausibles, puis présentent également les techniques d’analyse à mettre en oeuvre afin de traiter adéquatement ces trois considérations méthodologiques. Le plan d’analyse présenté plus loin dans le présent article intègre ces techniques recommandées. Au besoin, le lecteur est invité à consulter Vohl et Loye (sous presse) et Vohl (2023, chap. 3) pour de plus amples détails.
Les échantillons
Dans cette recherche, deux échantillons sont analysés : 1) le sous-échantillon d’élèves québécois en provenance d’écoles dont le français était la langue principale d’enseignement lors du PISA de 2003, issu de l’échantillon canadien du PISA de 2003 et 2) le sous-échantillon d’élèves québécois en provenance d’écoles dont le français était la langue principale d’enseignement lors du PISA de 2012, issu de l’échantillon canadien du PISA de 2012. Les échantillons canadiens du PISA de 2003 et de 2012 ont été générés selon un plan d’échantillonnage complexe, soit un plan d’échantillonnage aléatoire stratifié à deux niveaux. Le plan d’analyse proposé plus loin prend en compte le plan d’échantillonnage complexe mis en oeuvre par le PISA en 2003 et en 2012.
Le sous-échantillon de participants québécois francophones de 2003 est constitué de 2 151 élèves de 15 ans[4], soit 1 102 filles et 1 049 garçons (51,2 % et 48,8 %, respectivement), provenant de 119 écoles. Le sous-échantillon de 2012 contient 2 385 élèves de 15 ans, soit 1 251 filles et 1 134 garçons (50,9 % et 49,1 %, respectivement), en provenance de 109 écoles.
Les outils de collecte de données et les aspects éthiques considérés
Lors des épreuves du PISA de 2003 et de 2012, les participants ont été invités à répondre à deux types de questionnaires : les épreuves cognitives et le questionnaire contextuel (OCDE, 2005b ; OCDE, 2014c). Les épreuves cognitives, de type papier-crayon[5], d’une durée de 120 minutes ont servi à évaluer la culture mathématique, la culture scientifique et la compréhension de l’écrit. Le questionnaire contextuel, de type papier-crayon, d’une durée de 30 minutes, a servi à documenter divers facteurs non-cognitifs liés aux performances dans les trois domaines évalués, mais principalement en mathématiques (le domaine majeur d’évaluation lors de ces deux cycles). L’anxiété mathématique a également été documentée au moyen du questionnaire contextuel.
Lors des enquêtes du PISA de 2003 et de 2012, le consentement écrit des parents a été exigé afin que les élèves puissent participer aux épreuves (dans l’ensemble des pays/économies où la réglementation en vigueur exigeait un tel consentement) (OCDE, 2005b, 2014c). Afin de pouvoir procéder à l’analyse secondaire des données du PISA de 2003 et de 2012, la présente recherche a obtenu un certificat éthique décerné par le Comité d’éthique de la recherche en éducation et en psychologie (CEREP) de l’Université de Montréal.
Les variables étudiées et les données analysées
Afin de mener la présente recherche, trois variables sont utilisées : le genre, l’anxiété mathématique et les performances en mathématiques. Les instruments de mesure employés par le PISA, afin d’appréhender chacune de ces variables sont décrits dans ce qui suit.
Le genre
En 2003 et en 2012, le PISA a documenté le genre des participants au moyen d’un item dichotomique[6].
L’anxiété mathématique
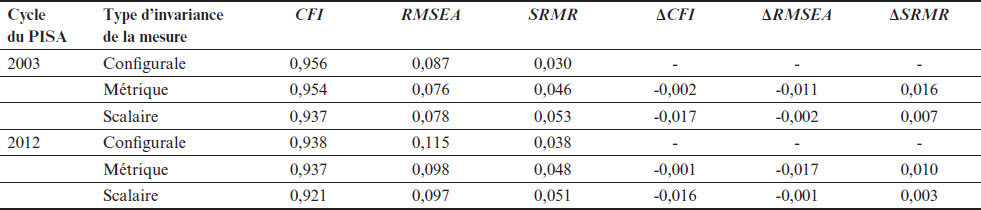
L’instrument de mesure de l’anxiété mathématique a été élaboré dans le cadre du PISA de 2003 et repris, de manière intégrale, en 2012. Les qualités psychométriques de l’instrument, telles que documentées par l’OCDE, font état d’un ajustement adéquat entre le modèle théorique et les données canadiennes. Elles font aussi état d’une fidélité adéquate (OCDE, 2005b, p. 293-294). Des analyses factorielles confirmatoires ont été effectuées, dans le cadre de la présente recherche, sur les échantillons d’élèves québécois francophones ayant participé au PISA de 2003 et de 2012. Ces analyses ont révélé un ajustement adéquat entre le modèle théorique et les données, sauf pour l’indice RMSEA qui révèle un mauvais ajustement puisque supérieur à 0,1 (Byrne, 2012) (pour 2003 : RMSEA = 0,116, CFI = 0,982, TLI = 0,963, SRMR = 0,026 ; pour 2012 : RMSEA = 0,140, CFI = 0,973, TLI = 0,946, SRMR = 0,032). Comme la majorité des indices révèlent un bon ajustement, l’usage des données n’est pas compromis par ces valeurs élevées de RMSEA. L’étude de fidélité a révélé des valeurs de ω respectives de 0,800 et 0,812, en 2003 et en 2012, ce qui témoigne d’une bonne fidélité de l’instrument de mesure de l’anxiété mathématique.
En outre, comme le premier objectif spécifique de recherche nécessite de procéder à des comparaisons multigroupes en regard de l’anxiété mathématique (comparaisons garçons vs filles, comparaisons 2003 vs 2012), nous avons mené préalablement des analyses factorielles confirmatoires multigroupes (Bollen, 1989 ; Hayduk, 1987 ; Jöreskog, 1971 ; Sörbom, 1974), de manière à vérifier l’invariance métrique et scalaire de la mesure d’anxiété mathématique. En effet, bien que peu de recherches jusqu’à aujourd’hui aient vérifié l’invariance métrique et scalaire de leurs instruments de mesure de l’anxiété mathématique, avant de comparer les moyennes observées entre les garçons et les filles (Rossi et al., 2022) ou avant de comparer les moyennes observées entre deux périodes, il est fortement recommandé de le faire afin de tirer des conclusions adéquates (Meredith, 1993 ; Steenkamp & Baumgartner, 1998 ; Steinmetz, 2011 ; Vandenberg & Lance, 2000). En effet, vérifier l’invariance scalaire est nécessaire avant de conclure que les écarts observés reflètent bien des écarts moyens du trait latent, puisqu’ils pourraient aussi refléter la non-invariance métrique et/ou la non-invariance scalaire, entre les groupes (voir Steinmetz, 2011 pour une explication détaillée).
Afin de vérifier l’invariance métrique et scalaire de l’instrument de mesure de l’anxiété mathématique, nous avons étudié les changements (Δ) des indices d’ajustement suivants : l’indice d’ajustement comparatif (CFI pour Comparative fit index, Bentler, 1990), la racine carrée de l’erreur quadratique moyenne d’approximation (RMSEA pour Root mean square error of approximation) et la valeur moyenne quadratique pondérée (SRMR pour Standardized Root Mean-Square Residual, Bentler, 1990), puis nous avons suivi les recommandations de Chen (2007).
Nous avons d’abord vérifié l’invariance des coefficients de saturation des items (invariance métrique) et appliqué la règle de décision suivante : un |∆CFI| ≥ 0,010 auquel s’ajoute un ∆RMSEA ≥ 0,015 ou un ∆SRMR ≥ 0,030 entre le modèle non-contraint et le modèle où les coefficients de saturation des items sont contraints à l’égalité indique de rejeter l’hypothèse de l’invariance métrique de la mesure (Chen, 2007, p. 501). Nous avons ensuite vérifié l’invariance des ordonnées à l’origine des items (invariance scalaire) et suivi la règle de décision suivante : un |∆CFI| ≥ 0,010 auquel s’ajoute un ∆RMSEA ≥ 0,015 ou un ∆SRMR ≥ 0,010, entre le modèle où les coefficients de saturation sont contraints à l’égalité et le modèle où les coefficients de saturation et les ordonnées à l’origine des items sont contraints à l’égalité, indique de rejeter l’hypothèse d’invariance scalaire de la mesure (Chen, 2007, p. 501).
Les résultats issus des analyses factorielles confirmatoires multigroupes menées (garçons vs filles en 2003 et en 2012, puis filles 2003 vs filles 2012 et garçons 2003 vs garçons 2012) sont présentés dans les tableaux 1 et 2. Les résultats ne nous permettent pas de rejeter l’hypothèse d’invariance scalaire de la mesure d’anxiété mathématique entre les filles et les garçons, pour 2003 et pour 2012. Il en est de même pour la mesure d’anxiété mathématique des filles en 2003 vs celle des filles en 2012, puis celle des garçons en 2003 vs celle des garçons en 2012. Ainsi, au moment de répondre à l’objectif spécifique 1, il sera adéquat de comparer les moyennes entre les filles et les garçons et entre 2003 et 2012, puis de présumer que les écarts observés reflètent bien des écarts du trait latent anxiété mathématique, entre ces groupes.
À partir des réponses fournies à chacun des items de l’indice de mesure de l’anxiété mathématique, le PISA calcule l’indice d’anxiété mathématique, un « […] indice élaboré sur la base des réponses des élèves concernant le stress et l’impuissance qu’ils peuvent ressentir face aux mathématiques » (OCDE, 2014b, p. 90). En 2003 et en 2012, une généralisation du modèle de Rasch à un paramètre (Rasch, 1960), le modèle de crédit partiel (Masters & Wright, 1997, cité dans OCDE, 2014c) a été utilisé pour la mise à l’échelle de chacun des items de l’instrument, puis une estimation ponctuelle de l’indice d’anxiété mathématique a été dérivée sur la base « d’une estimation pondérée des réponses les plus vraisemblables (weighted likelihood estimate, WLE) (Warm, 1989) » (OCDE, 2014b, p. 199). L’indice d’anxiété mathématique a été calculé et calibré de manière à ce que la moyenne, dans les pays de l’OCDE, soit de 0 et l’écart type de 1.
Au cycle de 2012, les valeurs de l’indice d’anxiété mathématique de 2003 ont été remises à l’échelle en utilisant les estimations des paramètres de l’enquête PISA 2012. En effet, afin de pouvoir comparer les données de 2003 et de 2012, les estimations pondérées (WLE) de 2003 ont été regénérées en utilisant les paramètres d’items de 2012 (OCDE, 2014b, p. 200). Ainsi, les indices d’anxiété mathématique de 2003, remis à l’échelle en 2012, sont les valeurs utilisées dans la présente recherche afin de documenter le niveau d’anxiété mathématique des participants du sous-échantillon de 2003[7].
En 2012, l’OCDE a employé le devis en trois formes (three-form design, Graham et al., 1996) au moment de constituer les questionnaires contextuels destinés aux élèves (OCDE, 2014c). Ce devis consiste à élaborer trois formes de questionnaires contextuels, puis à inclure certains des instruments de mesure dans uniquement deux des trois formes. Comme chaque participant ne répond qu’à une des trois formes de questionnaire, un tiers des données sont manquantes minimalement pour les instruments de mesure concernés. Le plan d’analyse de données présenté plus loin prévoit une procédure afin de traiter adéquatement les données manquantes générées par le devis en trois formes.
Les performances en mathématiques
Depuis 2003, en mathématiques, le PISA s’intéresse à une compétence appelée la « culture mathématique ». Cette compétence est définie comme « l’aptitude d’un individu à formuler, employer et interpréter des mathématiques dans un éventail de contextes, c’est-à-dire à raisonner en termes mathématiques et à utiliser des concepts, procédures, faits et outils mathématiques pour décrire, expliquer et prévoir des phénomènes. Elle aide les individus à comprendre le rôle que les mathématiques jouent dans le monde et à se comporter en citoyens constructifs, engagés et réfléchis, c’est-à-dire à poser des jugements et à prendre des décisions en toute connaissance de cause » (OCDE, 2014a, p. 42). Pour des exemples d’items, veuillez voir OCDE (2014a, p. 134-151).
Afin de rendre compte du niveau de compétence de chacun des candidats en regard de la culture mathématique, le PISA fournit cinq valeurs plausibles[8]. L’approche des valeurs plausibles est employée depuis 2000 par le PISA. Les données de 2003 ont été calibrées de sorte que, pour l’ensemble des pays de l’OCDE, la moyenne des cinq valeurs plausibles soit de 500 et l’écart type de 100. Pour toute analyse impliquant les performances, les cinq valeurs plausibles doivent être combinées selon l’approche de Little et Rubin (2002). Cette méthode est intégrée au plan d’analyses présenté plus loin. Mentionnons aussi qu’à partir des cinq valeurs plausibles, chaque participant est classé selon un niveau de compétence, à partir d’une échelle globale à six niveaux, élaborée par le PISA (voir OCDE, 2014a, p. 298).
Les procédures ayant permis d’obtenir les données des échantillons d’élèves québécois francophones ayant participé au PISA de 2003 et de 2012
Pour 2012, la base de données internationale du PISA a été téléchargée à partir de l’adresse https://www.oecd.org/pisa/data/pisa2012database-downloadabledata.htm[9]. Pour 2003, comme le Canada avait décidé, à l’époque, de ne pas rendre publique l’information relative à la province, dans la base de données internationale du PISA, une demande de renseignement a été soumise au Conseil des ministres de l’Éducation (Canada). Celui-ci nous a transmis la base de données de l’échantillon d’élèves québécois du PISA de 2003.
Les valeurs de l’indice d’anxiété mathématique de 2003, remises à l’échelle en 2012, ont été téléchargées à partir de l’adresse http://www.oecd.org/pisa/keyfindings/indices_2003.zip[10].
Tableau 1
Étude de l’invariance de la mesure d’anxiété mathématique entre les filles et les garçons francophones du Québec, pour 2003 et pour 2012
Note.CFI = indice d'ajustement comparatif (Comparative Fit Index), RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation (Root-Mean Square Error of Approximation), SRMR = valeur moyenne quadratique pondérée (Standardized Root Mean Square Residual), ∆ = changement.
Tableau 2
Étude de l’invariance de la mesure d’anxiété mathématique pour les filles francophones du Québec entre 2003 et 2012 et pour les garçons francophones du Québec entre 2003 et 2012
Note.CFI = indice d'ajustement comparatif (Comparative Fit Index), RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation (Root-Mean Square Error of Approximation), SRMR = valeur moyenne quadratique pondérée (Standardized Root Mean Square Residual), ∆ = changement.
L’analyse des données
Le traitement des trois considérations méthodologiques inhérentes aux enquêtes PISA
Afin de traiter adéquatement la première considération méthodologique inhérente aux enquêtes PISA, soit le fait que les données à analyser sont issues d’un plan d’échantillonnage complexe, il est suggéré de se tourner vers l’une ou l’autre des deux approches de modélisation suivantes : l’approche orientée devis et l’approche orienté modèle. Stapleton (2013) préconise l’approche orientée devis lorsque la non-indépendance des observations, inhérente au plan d’échantillonnage complexe, est considérée davantage comme une nuisance que comme un élément à modéliser, ce qui est le cas dans la présente étude. En effet, notre recherche vise à quantifier les écarts d’anxiété mathématique selon le genre et à étudier le lien anxiété mathématique/performances en mathématiques chez les élèves québécois, en tenant compte du fait que les données ne peuvent être considérées indépendantes (les élèves sont nichés à l’intérieur des écoles), sans chercher à modéliser la dépendance entre ces données (comparer le niveau moyen d’anxiété mathématique entre les écoles). De ce fait, dans la présente étude, nous privilégions l’approche orientée devis.
Conformément à ce que l’approche orientée devis préconise, pour toute estimation de paramètre, les observations des participants sont pondérées par les poids de sondage des élèves, des valeurs fournies dans les bases de données du PISA de 2003 et de 2012. En outre, afin d’estimer la variance de ces paramètres, les poids de sondage répliqués des élèves sont employés, des valeurs aussi fournies dans les bases de données du PISA de 2003 et de 2012[11].
Afin de traiter adéquatement la deuxième considération méthodologique inhérente aux enquêtes PISA (le fait que les données relatives à l’anxiété mathématique issues du PISA de 2012 ont été recueillies à l’aide d’un devis en trois formes et comportent ainsi minimalement un tiers de données manquantes), la méthode de vraisemblance maximale (full information maximum likelihood, FIML) est employée afin de procéder à l’ensemble des analyses. Enfin, de manière à traiter adéquatement la troisième considération méthodologique inhérente aux enquêtes PISA (le fait que le PISA utilise l’approche des valeurs plausibles afin de rendre compte du niveau d’habileté), pour toutes les estimations dans lesquelles les performances sont impliquées, l’approche de Little et Rubin (2002) est employée afin de combiner adéquatement les estimations faites avec chacune des cinq valeurs plausibles.
L’ensemble des analyses sont menées à l’aide du logiciel Mplus Version 8 qui présente les particularités suivantes : 1) il prend en charge les poids de sondage et les poids de sondage répliqués des élèves, 2) il intègre la méthode de vraisemblance maximale (Arbuckle, 1996 ; Little & Rubin, 2002) de manière à traiter adéquatement les données manquantes « en conjonction avec l’estimateur ML » (notre traduction de Wang et Wang, 2020, p. 47), l’estimateur de vraisemblance maximale et enfin, 3) il prend en charge les valeurs plausibles qu’il traite selon l’approche de Little et Rubin (2002). Pour traiter adéquatement le tout, Mplus Version 8 utilise l’estimateur MLR[12] (Maximum likelihood robust, Muthén & Muthén, 2017).
Le plan d’analyse des données
Les analyses menées afin de répondre à l’objectif spécifique 1
Afin de quantifier les écarts d’anxiété mathématique entre les filles et les garçons québécois francophones de 15 ans ayant participé au PISA en 2003 et en 2012, nous calculons la proportion de participants tout à fait en accord ou en accord avec chacun des items de l’instrument d’anxiété mathématique, selon le genre. Ensuite, nous calculons l’indice moyen d’anxiété mathématique selon le genre et comparons les moyennes à l’aide d’un test d’hypothèses sur une différence de moyennes. Nous calculons aussi l’indice moyen d’anxiété mathématique à chacun des niveaux de compétence, selon le genre, et comparons les moyennes à l’aide d’un test d’hypothèse sur une différence de moyennes.
Pour l’ensemble de ces tests d’hypothèses, en posant θfilles et θgarçons, la moyenne des filles et la moyenne des garçons respectivement, l’hypothèse nulle H0 et l’hypothèse alternative H1 sont données par (OCDE, 2009, p. 150) :
H0 : = ϴ filles – ϴ garçons = 0 et H1 : = ϴ filles – ϴ garçons ≠ 0,
puis la statistique de test est donnée par
avec ![]() et
et ![]() , les moyennes estimées chez les filles et les garçons
respectivement, puis
, les moyennes estimées chez les filles et les garçons
respectivement, puis ![]() , l’erreur type de la différence
, l’erreur type de la différence ![]() obtenue par
obtenue par
puisque les données des filles et celles des garçons ne peuvent être considérées indépendantes.
Pour les différences d’indice moyen d’anxiété mathématique statistiquement significatives, les tailles d’effet associées à ces différences observées sont calculées. Pour ce faire, conformément à ce que suggère l’OCDE (2009, p. 191), nous appliquons la formule suivante :
La tendance 2003-2012 de l’écart d’anxiété mathématique selon le genre est étudiée au moyen d’un test d’hypothèse sur une différence de moyenne. En posant δ2013 et δ2012, les écarts d’anxiété mathématique selon le genre de 2003 et de 2012 respectivement, l’hypothèse nulle H0 et l’hypothèse alternative H1 sont données par (OCDE, 2009, p. 150) :
H0 : = δ 2012 – δ 2003 = 0 et H1 : = δ 2012 – δ 2003 ≠ 0
puis la statistique de test est donnée par
avec
car les données issues de deux cycles différents du PISA peuvent être considérées indépendantes (OCDE, 2009, p. 175).
Les analyses menées afin de répondre à l’objectif spécifique 2
Afin de vérifier si le lien anxiété mathématique/performance est négatif, nous définissons les performances comme variable dépendante et l’anxiété mathématique comme variable indépendante dans un modèle de régression linéaire simple. Ce modèle de régression est donné par l’expression suivante :
Performances = β0 + β1 • ANXMAT .
Afin de vérifier si le genre modère le lien anxiété mathématique/performances en mathématiques, nous définissons un second modèle de régression. Celui-ci inclut deux variables indépendantes, la variable anxiété mathématique et la variable genre, de même que le terme d’interaction entre ces deux variables. Le modèle est donné par l’expression :
Performances = β0 + β1 • ANXMAT + β2 • genre + β3 • ANXMAT * genre
Dans ce modèle, nous vérifions si le coefficient β3 est significatif. S’il est non significatif, nous concluons que le genre ne modère pas le lien anxiété mathématique/performances en mathématiques.
Résultats
Les statistiques descriptives des trois variables étudiées, puis la proportion de données manquantes relatives à chacune de ces variables sont présentées aux annexes B2 et B3, dans Vohl (2023).
Les résultats en lien avec OS1
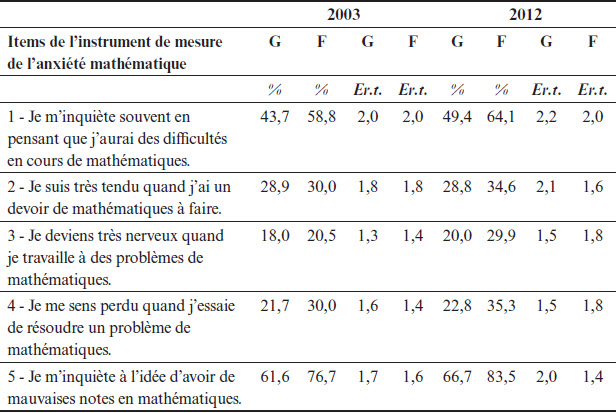
Afin de comparer le niveau d’anxiété mathématique des élèves québécois francophones de 15 ans ayant participé au PISA en 2003 et en 2012, selon le genre, trois tableaux sont présentés (tableaux 3, 4 et 5). Le tableau 3 rapporte, pour 2003 et 2012, le pourcentage de participants qui se sont dits tout à fait en accord ou en accord avec les items de l’instrument de mesure de l’anxiété mathématique, selon le genre. Les résultats montrent, pour 2003 et pour 2012, des pourcentages plus élevés chez les filles, pour les cinq items.
Tableau 3
Pourcentage des participants qui se sont dits tout à fait en accord ou en accord avec les items de l’instrument d’anxiété mathématique en 2003 et en 2012
Le tableau 4 révèle, pour 2003 et 2012, l’écart dans le niveau moyen d’anxiété mathématique des filles et des garçons, de même que la tendance 2003-2012 de cet écart. Les résultats montrent qu’en 2003 et en 2012, les filles québécoises francophones ont obtenu un indice moyen d’anxiété mathématique supérieur à celui des garçons québécois francophones. Dans les deux cas, les écarts observés, selon le genre, se sont avérés statistiquement significatifs avec des tailles d’effet respectives de 0,33 et de 0,43. En outre, la tendance 2003-2012 de l’écart d’anxiété mathématique selon le genre, une valeur statistiquement significative de 0,12, révèle que la disparité d’anxiété mathématique selon le genre est un phénomène qui s’est accentué entre 2003 et 2012, chez les élèves québécois francophones ayant participé au PISA.
Le tableau 5 fait état des écarts d’anxiété mathématique, selon le genre, à chacun des niveaux de compétence atteint par les participants. Les résultats montrent qu’à chacun des niveaux de l’échelle de compétence du PISA, les filles se sont dites davantage anxieuses à l’égard des mathématiques que les garçons. Ces résultats révèlent en outre qu’à l’exception des niveaux 5 et 6 en 2003, l’ensemble des écarts d’anxiété mathématique observés, selon le genre, se sont avérés statistiquement significatifs (p < 0,1). La comparaison des écarts observés en 2003 et en 2012 ne nous permet toutefois pas d’identifier un niveau de compétence où les écarts se seraient avérés les plus marqués à la fois en 2003 et en 2012.
Tableau 4
Niveau moyen d’anxiété mathématique chez les participants du PISA de 2003 et du PISA de 2012, selon le genre, écarts selon le genre et tendance 2003-2012 des écarts selon le genre
Note. G = garçons, F = filles, M = moyenne, Er.t. = erreur type, p = valeur p, d = taille d’effet, ANXMAT = anxiété mathématique.
Tableau 5
Écarts du niveau moyen d’anxiété mathématique chez les participants du PISA de 2003 et du PISA de 2012, selon le genre, à chacun des niveaux de compétence de l’échelle de compétence du PISA
Note. G = garçons, F = filles, M = moyenne, Er.t. = erreur type, p = valeur p, ANXMAT = anxiété mathématique.
Les résultats en lien avec OS2
Les résultats des analyses menées afin de vérifier si le lien anxiété mathématique/performance est négatif et si le genre modère ce lien, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, sont présentés dans les tableaux 6 et 7. Les résultats du tableau 6 révèlent qu’en 2003 et en 2012, le coefficient de régression de la variable anxiété mathématique s’est révélé négatif. Les résultats montrent aussi que la baisse de performance en mathématiques associée à une hausse d’une unité de l’indice d’anxiété mathématique a été de 36,81 points en moyenne, chez les élèves francophones du Québec de 15 ans en 2003 et de 31,73 points, en moyenne, en 2012. Le coefficient de corrélation linéaire entre l’anxiété mathématique et les performances en mathématiques s’élève à -0,36 en 2003 et à -0,34 en 2012. La variation de l’anxiété mathématique explique 13 % de la variation des performances en mathématiques des élèves québécois francophones en 2003 et 11,8 % en 2012.
Les résultats du tableau 7 révèlent que le coefficient de régression de l’interaction entre l’anxiété mathématique et le genre est non significatif. De ce fait, le lien anxiété mathématique/performances en mathématiques peut être considéré équivalent chez les garçons et les filles : il n’y a pas lieu de penser que le genre modère la relation anxiété mathématique/performances en mathématiques, chez les élèves québécois francophones de 15 ans.
Tableau 6
Résultats du premier modèle de régression linéaire chez l’ensemble des élèves québécois francophones ayant participé au PISA de 2003 et de 2012
Note. β0= valeur estimée de l’ordonnée à l’origine, β1= valeur estimée du coefficient de régession de la variable anxiété mathématique, Er.t. = erreur type, p = valeur p, r = coefficient de corrélation linéaire, R2= coefficient de détermination, ANXMAT = anxiété mathématique.
Tableau 7
Résultats du second modèle de régression linéaire chez l’ensemble des élèves québécois francophones ayant participé au PISA de 2003 et de 2012
Note. β0= valeur estimée de l’ordonnée à l’origine, β1= valeur estimée du coefficient de régession de la variable anxiété mathématique, β2= valeur estimée du coefficient de régression de la variable genre, β3= valeur estimée du coefficient de régression de l’interaction des variables anxiété mathématique et genre, Er.t. = erreur type, p = valeur p, R2= coefficient de détermination, ANXMAT = anxiété mathématique.
Discussion
L’objectif général de cet article visait à quantifier les écarts d’anxiété mathématique selon le genre et à étudier le lien anxiété mathématique/performances en mathématiques, chez les élèves québécois francophones de 15 ans, à partir d’une analyse secondaire des données du PISA de 2003 et de 2012. Cette recherche a été menée afin de vérifier si l’anxiété mathématique pourrait être un phénomène qui contribue aux écarts de performance observés entre les garçons et les filles en mathématiques au Québec. Pour ce faire, notre objectif général de recherche a été opérationnalisé en deux objectifs spécifiques. Le premier a consisté à quantifier les écarts d’anxiété mathématique des filles et des garçons francophones de 15 ans du Québec ayant participé au PISA en 2003 et en 2012 et à documenter la tendance 2003-2012 de ces écarts. Le second objectif a visé à vérifier si le lien linéaire anxiété mathématique/performances en mathématiques est négatif et si le genre modère ce lien, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et à celui de 2012.
Après avoir vérifié l’invariance métrique et scalaire de la mesure d’anxiété mathématique du PISA, entre les garçons et les filles francophones du Québec et entre 2003 et 2012, nos résultats ont montré, à la fois en 2003 et en 2012, que les filles québécoises francophones se sont dites davantage anxieuses à l’égard des mathématiques que les garçons. Qui plus est, les filles francophones de 15 ans du Québec se sont également dites davantage anxieuses à l’égard des mathématiques que les garçons à tous les niveaux de l’échelle de compétence du PISA, sauf dans les niveaux 5 et 6 en 2003 (ce dernier résultat est difficilement interprétable dans le présent contexte d’autant plus qu’il ne s’est pas reproduit en 2012). Ainsi, de manière générale, même à compétence égale, les filles francophones du Québec ont fait état d’un niveau moyen d’anxiété mathématique plus élevé que les garçons.
Nos résultats ont en outre permis d’objectiver, chez les élèves québécois francophones, la présence d’un lien linéaire négatif entre l’anxiété mathématique et les performances en mathématiques. Ainsi, nous avons confirmé, chez ces élèves, la présence de deux phénomènes documentés de manière robuste dans les écrits, à savoir un niveau moyen d’anxiété mathématique plus élevé chez les filles que chez les garçons, à tout le moins, à partir de l’adolescence (Else-Quest et al., 2010 ; Hyde et al., 1990 ; Stoet et al. 2016) et la présence d’un lien négatif anxiété mathématique/performances en mathématiques (Barroso et al., 2021 ; Hembree, 1990 ; Ma, 1999 ; Zhang et al., 2019). En outre, à l’égard de ce lien, nous avons montré qu’il n’y a pas lieu de penser que le genre le modère, chez les élèves québécois francophones. D’un point de vue pratique, ce résultat permet d’affirmer que, pour une augmentation d’une unité de l’indice d’anxiété mathématique, les performances des filles diminuent de manière équivalente à celles des garçons, en mathématiques.
La comparaison des écarts d’anxiété mathématique observés chez les élèves québécois francophones et ceux observés dans les autres pays/économies membres de l’OCDE montrent que les écarts observés chez les élèves québécois francophones sont particulièrement marqués. En effet, en 2003, seulement 14 pays/économies membres de l’OCDE sur 29 ont rapporté des écarts d’anxiété mathématique selon le genre aussi élevés que ceux révélés chez les élèves québécois francophones (OCDE, 2004, tableau 3.8). En 2012, seulement six pays/économies membres de l’OCDE sur 34 l’ont fait (OCDE, 2014b, annexe B1, tableau III.4.3d). De surcroît, alors que la disparité d’anxiété mathématique selon le genre s’est accrue de 0,12 (p < 0,05) chez les élèves québécois francophones de 15 ans entre 2003 et 2012, pendant cette même période, elle s’est accrue de 0,06 en moyenne au Canada (p > 0,05) et de 0,03 en moyenne dans les pays de l’OCDE (p < 0,05). Sur 29 pays membres de l’OCDE, seul le Danemark a connu une progression de l’écart d’anxiété mathématique selon le genre plus marquée que celle observée chez les élèves québécois francophones. Le Danemark a enregistré une hausse significative de 0,14 de cet écart entre 2003 et 2012 (OCDE, 2014b, annexe B1, tableau III.4.3g).
À la manière des résultats issus des méta-analyses citées dans cet article, nos résultats doivent toutefois être interprétés avec circonspection. En effet, la nature transversale des données analysées dans notre recherche ne nous permet pas de conclure à l’existence d’une relation causale entre l’anxiété mathématique et les performances en mathématiques. Nos résultats révèlent des associations qui ne peuvent qu’être interprétées comme telles.
Également, tout comme dans les méta-analyses citées dans cet article, l’idée selon laquelle les écarts d’anxiété mathématique observés selon le genre puissent s’expliquer par des considérations méthodologiques ne peut être exclue (Devine et al., 2012 ; Frenzel et al., 2007 ; Hill et al., 2016). En effet, il est possible, par exemple, que les filles rapportent un niveau moyen d’anxiété mathématique supérieur à celui des garçons simplement parce que les filles sont, de manière générale, plus à l’aise, capables ou ouvertes à rapporter leurs émotions que les garçons (Ashcraft, 2002 ; Ashcraft et Ridley, 2005 ; Bryant et al., 1996 ; Devine et al., 2012 ; Frenzel et al., 2007 ; Hunsley & Flessati, 1988). Cette aisance peut en outre être amplifiée par des phénomènes tels que les stéréotypes de genre en mathématiques (p.ex., « les garçons sont meilleurs que les filles en mathématiques ») ou encore, la désirabilité sociale (Frenzel et al., 2007). En effet, les instruments de mesure auto-rapportée, comme ceux employés afin de documenter l’anxiété mathématique, depuis les années 1970, sont reconnus pour leur vulnérabilité à divers types de biais tels que le biais de réponse lié au genre (gender-linked response bias) (Devine et al., 2012, p. 6), le biais de désirabilité sociale (Paulhus, 2017) ou encore le biais de réponse attribuable au calibrage inadéquat des perceptions et des jugements relatifs à l’apprentissage, chez les élèves (Winne & Jamieson-Noel, 2002), etc.
La disparité d’anxiété mathématique selon le genre, observée dans le cadre de notre recherche, pourrait aussi s’expliquer par des différences générales d’anxiété, entre les garçons et les filles (Dowker et al., 2016 ; Frenzel et al., 2007 ; Hill et al., 2016). En effet, des études indiquent que les filles ont, en moyenne, un niveau d’anxiété générale[13] supérieur à celui des garçons (Chapman et al, 2007 ; Costa et al., 2001 ; Feingold, 1994 ; Szczygiel, 2020). Toutefois, des études révèlent que, même en contrôlant l’anxiété générale, les filles se disent en moyenne davantage anxieuses que les garçons (Delage et al., 2022 ; Ferguson et al., 2015).
En outre, comme l’anxiété mathématique a été appréhendée au moyen d’un questionnaire auto-rapporté de type trait et que ce type de questionnaire auto-rapporté est plus susceptible d’être biaisé par le concept de soi que les questionnaires auto-rapportés de type état (Goetz et al., 2013 ; Robinson & Clore, 2002), les écarts d’anxiété mathématique observés selon le genre pourraient aussi s’expliquer, au moins partiellement, par le fait que les filles révèlent, de manière générale, un concept de soi plus faible que les garçons, en moyenne, sans toutefois que le niveau d’anxiété mathématique de type état diffère selon le genre.
Cependant, même s’il advenait que la disparité d’anxiété mathématique selon le genre s’explique en tout ou en partie par l’anxiété générale ou par l’une ou l’autre des considérations méthodologiques énoncées ci-haut, le phénomène n’en demeure pas moins important. En effet, comparativement aux personnes qui se disent faiblement ou pas anxieuses, celles qui se disent davantage anxieuses à l’égard des mathématiques sont susceptibles de moins bien réussir en mathématiques et risquent, en outre, de se diriger dans une mesure moindre vers les professions liées aux mathématiques (Stoet et al., 2016). Ces constats ont des implications pratiques et scientifiques importantes. En effet, dans un premier temps, ils invitent à poursuivre le travail amorcé dans cet article en cherchant à identifier des facteurs qui pourraient permettre éventuellement de réduire les écarts d’anxiété mathématique observés entre les filles et les garçons, au Québec. Dans un second temps, ils invitent à se pencher sur les stratégies d’intervention qui pourraient permettre de réduire, notamment, l’importance du lien négatif anxiété mathématique/performances en mathématiques, chez les personnes qui se disent anxieuses à l’égard des mathématiques.
Un article subséquent (Vohl & Loye, 2024, accepté) vise justement à identifier des facteurs qui pourraient expliquer les écarts d’anxiété mathématique selon le genre et qui ont le potentiel de guider la mise en oeuvre d’interventions visant à les réduire. En effet, dans cet article subséquent, en prenant appui sur le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006), nous vérifions si trois perceptions de nature motivationnelle (le concept de soi, la valeur intrinsèque accordée aux mathématiques et la valeur utilitaire des mathématiques) peuvent expliquer en partie les écarts d’anxiété mathématique observés entre les garçons et les filles francophones du Québec de 15 ans ayant participé au PISA de 2003 et de 2012.
En ce qui concerne les stratégies d’intervention qui pourraient permettre de réduire l’importance du lien négatif anxiété mathématique/performances en mathématiques, la méta-analyse d’Hembree (1990) a révélé que les interventions à privilégier sont : 1) la désensibilisation systématique par l’exposition aux mathématiques, 2) la restructuration cognitive, une approche qui vise à identifier les pensées négatives, à les réévaluer et à les modifier et, enfin, 3) la thérapie cognitivo-comportementale, qui combine la restructuration cognitive et la désensibilisation systématique ou la restructuration cognitive et l’entraînement à la relaxation. Depuis la publication de cette méta-analyse, quelques rares recherches (Passolunghi et al., 2020), expérimentales ou quasi-expérimentales, ont été menées de manière à vérifier l’efficacité de stratégies d’interventions en lien avec l’anxiété mathématique. Ces quelques recherches ont obtenu des résultats prometteurs : elles ont montré des réductions du niveau d’anxiété mathématique, chez des enfants de 1re et de 2e année et chez des adultes (Jamieson et al., 2016 ; Park et al., 2014 ; Passolunghi et al., 2022 ; Supekar et al., 2015), de même que des réductions du lien négatif anxiété mathématique/performances chez des adultes (Jamieson et al., 2016 ; Park et al., 2014 ; Passolunghi et al., 2022).
Les limites
Avant de conclure, nous tenons à souligner la limite suivante. « Dans l’optique de réduire au minimum le risque de biais de réponse, les normes de qualité des données du PISA exigent des taux minimums de participation pour les écoles et les élèves. À l’échelle du Canada, un taux de réponse minimum de 85 p. 100 était exigé pour les écoles sélectionnées initialement » (O’Grady et al., 2016, p. 53). « Le PISA exige en outre un taux de participation minimum des élèves de 80 p. 100 dans l’ensemble des écoles participantes (échantillon initial et échantillon de remplacement) à l’échelle du pays » (O’Grady et al., 2016, p. 53). Or, en 2012, au Québec, le taux de participation des écoles au PISA a été supérieur au seuil minimal requis, mais le taux de réponse des élèves a été de 75,6 %, une valeur inférieure au seuil de 80 % fixé par l’OCDE (Brochu et al., 2013). De ce fait, les résultats de 2012 doivent être considérés avec circonspection. Toutefois, une analyse des caractéristiques de répondants et des non-répondants a révélé que le phénomène « […] pourrait avoir une incidence marginale sur les résultats du Québec […] » (Brochu et al., 2013, p. 55-56).
Conclusion
À partir des données du PISA de 2003 et de 2012, nous avons quantifié les écarts d’anxiété mathématique selon le genre et étudié le lien anxiété mathématique/performances en mathématiques, chez les élèves québécois francophones de 15 ans, à partir d’une analyse secondaire des données du PISA de 2003 et de 2012. Il s’agit, à notre connaissance, du premier portrait fourni en la matière chez les élèves québécois francophones. Nos résultats ont montré qu’en 2003 et en 2012, les filles québécoises francophones se sont dites davantage anxieuses à l’égard des mathématiques que les garçons. De plus, ils ont montré que le lien anxiété mathématique est un lien négatif et équivalent, chez les filles et chez les garçons. De là, nous concluons que la disparité d’anxiété mathématique selon le genre pourrait contribuer à expliquer les écarts de performances observés entre les garçons et les filles, dans le cadre des divers cycles du PISA, depuis l’année 2000. Dans un article subséquent (Vohl & Loye, 2024, accepté), nous étudions trois perceptions de l’apprenant mises en cause pour expliquer la disparité d’anxiété mathématique selon le genre. Ces facteurs pourront, à terme, fournir des leviers en vue de réduire les écarts d’anxiété mathématique observés entre les filles et les garçons francophones du Québec.
Appendices
Notes
-
[1]
Dans l’article de Fonseca et al. (2021), la définition de la numératie est celle retenue dans le cadre du Programme pour l’évaluation des compétences des adultes, à savoir « la capacité de localiser, d’utiliser, d’interpréter et de communiquer de l’information et des idées mathématiques afin de s’engager et de gérer les demandes mathématiques de tout un éventail de situations de la vie adulte » (OCDE, 2014d, p. 27).
-
[2]
Le TIMSS, mis en oeuvre depuis 1995 par l’International Association for the Evaluation of Educational Achievement (IEA), mesure tous les quatre ans les performances en mathématiques et en sciences des élèves de la 4e et de la 8e année de scolarité obligatoire. Les élèves sont alors âgés de 10 ans et de 14 ans, respectivement.
-
[3]
Le PISA, mis en oeuvre par l’OCDE depuis 2000, mesure tous les trois ans les performances des élèves de 15 ans dans les trois domaines suivants : culture mathématique, culture scientifique et compréhension de l’écrit.
-
[4]
Les participants du PISA avaient entre « […] 15 ans et 3 mois révolus et 16 ans et 2 mois révolus au moment de l’évaluation » (OCDE, 2014a, p. 29).
-
[5]
En 2012, une épreuve cognitive informatisée a été introduite, mais les résultats analysés dans cette recherche sont ceux issus des épreuves papier-crayon.
-
[6]
L’item ST03Q01 en 2003 et l’item ST01Q04, en 2012.
-
[7]
Dans les bases de données du PISA de 2003 et de 2012, l’indice d’anxiété mathématique est donné par la variable ANXMAT, puis les cinq items de l’instrument sont identifiés par ST32Q01, ST32Q03, ST32Q05, ST32Q08 et ST32Q10 en 2003 et ST42Q01, ST42Q03, ST42Q05, ST42Q08 et ST42Q10 en 2012.
-
[8]
Dans les bases de données du PISA de 2003 et de 2012, les cinq valeurs sont identifiées par les variables PV1MATH, PV2MATH, PV3MATH, PV4MATH et PV5MATH.
-
[9]
Les élèves canadiens ont été identifiés par la variable CNT=CAN, puis les élèves québécois francophones ont été identifiés par la variable STRATUM = CAN0545 ou CAN0546 ou CAN0547, tel que le suggère le livre de code du PISA 2012, https://www.oecd.org/pisa/pisaproducts/PISA12_stu_codebook.pdf.
-
[10]
Les valeurs de 2003 remises à l’échelle en 2012 ont été fusionnées à la base de données de l’échantillon d’élèves québécois francophones de 2003 à l’aide de deux identifiants : la variable SCHOOLID (l’identifiant de l’école) et la variable STIDSTD (l’identifiant de l’élève).
-
[11]
Les poids de sondage des élèves sont identifiés par la variable W_FSTUWT dans ces bases de données, puis les poids de sondage répliqués par W_FSTR1 à W_FSTR80 (80 poids de sondage répliqués).
-
[12]
« L’estimateur MLR est l’estimateur de vraisemblance maximale qui estime les paramètres, leur erreur type et la statistique du chi carré de manière à ce qu’ils soient robustes à la non-normalité et à la non-indépendance des observations lorsqu’ils sont utilisés avec TYPE = COMPLEX » [notre traduction] (Muthén & Muthén, 2017, p. 668). TYPE = COMPLEX est utilisé ici car le plan d’échantillonnage est un plan d’échantillonnage complexe (Vohl & Loye, sous presse ; Vohl, 2023, chap. 3).
-
[13]
L’anxiété générale (general anxiety) est une disposition individuelle qui se caractérise par le fait de s’inquiéter à propos des événements, de ses comportements et de ses compétences personnelles (Spence, 1997).
Liste des références
- Alexander, L. & Martray, C. (1989). The development of an abbreviated version of the Mathematics Anxiety Rating Scale. Measurement Evaluation in Counseling Development, 22(3), 143-150. https://doi.org/10.1080/07481756.1989.12022923
- Arbuckle, J. L. (1996). Full information estimation in the presence of incomplete data. Dans G. A. Marcoulides & R. E. Schumacker (dir.), Advanced structural equation modeling: Issues and techniques (p. 243-277). Lawrence Erlbaum Associates, Inc.
- Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181-185. https://doi.org/10.1111/1467-8721.00196
- Ashcraft, M. H. & Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General, 130(2), 224-237. https://doi.org/10.1037/0096-3445.130.2.224
- Ashcraft, M. H. & Moore, A. M. (2009). Mathematics anxiety and the affective drop in performance. Journal of Psychoeducational assessment, 27(3), 197-205. https://doi.org/10.1177/0734282908330580
- Ashcraft, M. H. & Ridley, K. S. (2005). Math anxiety and its cognitive consequences: A tutorial review. Dans J. I. D. Campbell (dir.), Handbook of Mathematical Cognition (p. 315-327). Psychology Press.
- Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A. & Daucourt, M. C. (2021). A meta-analysis of the relation between math anxiety and math achievement. Psychological Bulletin, 147(2), 134-168. https://doi.org/10.1037/bul0000307
- Beilock, S. L. & Maloney, E. A. (2015). Math anxiety: A factor in math achievement not to be ignored. Policy Insights from the Behavioral and Brain Sciences, 2(1), 4-12. https://doi.org/10.1177/2372732215601438
- Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107(2), 238-246. https://doi.org/10.1037/0033-2909.107.2.238
- Bollen, K. A. (1989). Structural equations with latent variables. John Wiley & Sons.
- Brochu, P., Deussing, M.-A., Houme, K. & Chuy, M. (2013). À la hauteur: Résultats canadiens de l›étude PISA de l›OCDE - Le rendement des jeunes du Canada en sciences, en lecture et en mathématiques - Premiers résultats de 2012 pour les jeunes du Canada âgés de 15 ans. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/318/PISA2012_CanadianReport_FR_Web.pdf
- Bryant, F. B., Yarnold, P. R. & Grimm, L. G. (1996). Toward a measurement model of the affect intensity measure: A three-factor structure. Journal of Research in Personality, 30(2), 223-247. https://doi.org/10.1006/jrpe.1996.0015
- Bussière, P., Knighton, T. & Cartwright, F. (2004). À la hauteur : résultats canadiens de l’études PISA de l’OCDE: la performance des jeunes du Canada en mathématiques, en lecture, en sciences et en résolution de problèmes: premiers résultats de 2003 pour les Canadiens de 15 ans. Statistique Canada. https://www.cmec.ca/docs/pisa2003.fr.pdf
- Byrne, B. M. (2012). Structural equation modeling with Mplus: Basic concepts, applications, and programming. Routledge.
- Chapman, B. P., Duberstein, P. R., Sörensen, S. & Lyness, J. M. (2007). Gender differences in Five Factor Model personality traits in an elderly cohort. Personality and individual differences, 43(6), 1594-1603. https://doi.org/10.1016/j.paid.2007.04.028
- Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural equation modeling: a multidisciplinary journal, 14(3), 464-504. https://doi.org/10.1080/10705510701301834
- Chiu, M. M. & Klassen, R. M. (2010). Relations of mathematics self-concept and its calibration with mathematics achievement: cultural differences among fifteen-year-olds in 34 countries. Learning Instruction, 20(1), 2-17. https://doi.org/10.1016/j.learninstruc.2008.11.002
- Cipora, K., Artemenko, C. & Nuerk, H.-C. (2019). Different ways to measure math anxiety. Dans I. C. Mammarella, S. Caviola & A. Dowker (dir.) Mathematics Anxiety – What is known and what is still to be understood (p. 20-41). Routledge.
- Costa Jr, P. T., Terracciano, A. & McCrae, R. R. (2001). Gender differences in personality traits across cultures: robust and surprising findings. Journal of personality and social psychology, 81(2), 322. https://doi.org/10.1037/0022-3514.81.2.322
- Delage, V., Trudel, G., Retanal, F. & Maloney, E. A. (2022). Spatial anxiety and spatial ability: Mediators of gender differences in math anxiety. Journal of Experimental Psychology: General, 151(4), 921-933. https://psycnet.apa.org/doi/10.1037/xge0000884
- Devine, A., Fawcett, K., Szűcs, D. & Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and brain functions, 8(1), 1-9. https://doi.org/10.1186/1744-9081-8-33
- Dowker, A., Bennett, K. & Smith, L. (2012). Attitudes to mathematics in primary school children. Child Development Research, 2012, Article 124939. https://doi.org/10.1155/2012/124939
- Dowker, A., Sarkar, A. & Looi, C. Y. (2016). Mathematics anxiety: What have we learned in 60 years? Frontiers in psychology, 7, Article 508, 1-16. https://doi.org/10.3389/fpsyg.2016.00508
- Else-Quest, N. M., Hyde, J. S. & Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychological bulletin, 136(1), 103. http://dx.doi.org/10.1037/a0018053
- Encinas-Martín, M. & Cherian, M. (2023). Gender, Education and Skills: The Persistence of Gender Gaps in Education and Skills, OECD Skills Studies. Éditions OCDE. https://doi.org/10.1787/34680dd5-en
- Faust, M. W. (1992). Analysis of physiological reactivity in mathematics anxiety. [thèse de doctorat, Bowling Green State University]. https://etd.ohiolink.edu/apexprod/rws_etd/send_file/send?accession=bgsu1668674996430557&disposition=inline
- Feingold, A. (1994). Gender differences in personality: a meta-analysis. Psychological bulletin, 116(3), 429. https://doi.org/10.1037/0033-2909.116.3.429
- Fennema, E. & Sherman, J. A. (1976). Fennema-Sherman mathematics attitudes scales: Instruments designed to measure attitudes toward the learning of mathematics by females and males. Journal for Research in Mathematics Education, 7(5), 324-326. https://doi.org/10.2307/748467
- Ferguson, A. M., Maloney, E. A., Fugelsang, J. & Risko, E. F. (2015). On the relation between math and spatial ability: The case of math anxiety. Learning Individual Differences, 39, 1-12. https://doi.org/10.1016/j.lindif.2015.02.007
- Fonseca, R., Fontaine, M. M. & Haeck, C. (2021). Le lien entre les compétences en numératie et les rendements sur le marché du travail au Québec (2021RP-11, CIRANO). https://www.cirano.qc.ca/fr/sommaires/2021RP-11
- Frenzel, A. C., Pekrun, R. & Goetz, T. (2007). Girls and mathematics—A “hopeless” issue? A control-value approach to gender differences in emotions towards mathematics. European Journal of Psychology of Education, 22(4), 497-514. https://doi.org/10.1007/BF03173468
- Geary, D. C. (1996). Sexual selection and sex differences in mathematical abilities. Behavioral and brain sciences, 19(2), 229-247. https://doi.org/10.1017/S0140525X00042400
- Goetz, T., Bieg, M., Lüdtke, O., Pekrun, R. & Hall, N. C. (2013). Do Girls Really Experience More Anxiety in Mathematics? Psychological Science, 24(10), 2079-2087. https://doi.org/10.1177%2F0956797613486989
- Gough, M. F. (1954). Why Failures in Mathematics? Mathemaphobia : Causes and Treatments. The Clearing House: A Journal of Educational Strategies, Issues and Ideas, 28(5), 290-294. https://doi.org/10.1080/00098655.1954.11476830
- Graham, J. W., Hofer, S. M. & MacKinnon, D. P. (1996). Maximizing the usefulness of data obtained with planned missing value patterns: An application of maximum likelihood procedures. Multivariate Behavioral Research, 31(2), 197-218. https://doi.org/10.1207/s15327906mbr3102_3
- Hayduk, L. A. (1987). Structural equation modeling with LISREL: Essentials and advances. Jhu Press.
- Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. Journal for Research in Mathematics Education, 21(1), 33-46. https://doi.org/10.2307/749455
- Hill, F., Mammarella, I. C., Devine, A., Caviola, S., Passolunghi, M. C. & Szűcs, D. (2016). Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning and individual differences, 48, 45-53. https://doi.org/10.1016/j.lindif.2016.02.006.
- Ho, H. Z., Senturk, D., Lam, A. G., Zimmer, J. M., Hong, S., Okamoto, Y., Chiu, S.-Y., Nakazawa, Y. & Wang, C. P. (2000). The affective and cognitive dimensions of math anxiety: A cross-national study. Journal for research in Mathematics Education, 31(3), 362-379. https://doi.org/10.2307/749811
- Hopko, D. R., Mahadevan, R., Bare, R. L. & Hunt, M. K. (2003). The abbreviated math anxiety scale (AMAS) construction, validity, and reliability. Assessment, 10(2), 178-182. https://doi.org/10.1177/1073191103010002008
- Hunsley, J. & Flessati, S. L. (1988). Gender and mathematics anxiety: The role of math-related experiences and opinions. Anxiety Research, 1(3), 215-224. https://doi.org/10.1080/08917778808248720
- Hyde, J. S., Fennema, E., Ryan, M., Frost, L. A. & Hopp, C. (1990). Gender comparisons of mathematics attitudes and affect: A meta-analysis. Psychology of women quarterly, 14(3), 299-324. https://doi.org/10.1111%2Fj.1471-6402.1990.tb00022.x
- Jacobs, J. K. & Morita, E. (2002). Japanese and American teachers’ evaluations of videotaped mathematics lessons. Journal for Research in Mathematics Education, 33(3), 154-175. https://doi.org/10.2307/749723
- Jamieson, J. P., Peters, B. J., Greenwood, E. J. & Altose, A. J. (2016). Reappraising Stress Arousal Improves Performance and Reduces Evaluation Anxiety in Classroom Exam Situations. Social Psychological and Personality Science, 7(6), 579–587. https://doi.org/10.1177/1948550616644656
- Joensen, J. S. & Nielsen, H. S. (2009). Is there a causal effect of high school math on labor market outcomes? Journal of Human Resources, 44(1), 171-198.
- Jöreskog, K. G. (1971). Simultaneous factor analysis in several populations. Psychometrika, 36(4), 409-426.
- Little, R. J. & Rubin, D. B. (2002). Statistical analysis with missing data (2e éd.). John Wiley & Sons.
- Lohr, S. L. (2019). Sampling: Design and Analysis (2e éd.). Chapman & Hall/CRC. https://doi.org/10.1201/9780429296284
- Lyons, I. M. & Beilock, S. L. (2012). When math hurts: math anxiety predicts pain network activation in anticipation of doing math. PloS One, 7(10), Article e48076. https://doi.org/10.1371/journal.pone.0048076
- Ma, X. (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education, 30(5), 520-540. https://doi.org/10.2307/749772
- Maloney, E. A. (2016). Math anxiety: Causes, consequences, and remediation. Dans K. R. Wentzel & D. B. Miele (dir.), Handbook of motivation at school (2e éd., p. 408-423). Routledge.
- Maloney, E. A., Ansari, D. & Fugelsang, J. A. (2011). The effect of mathematics anxiety on the processing of numerical magnitude. The Quarterly Journal of Experimental Psychology, 64(1), 10-16. https://doi.org/10.1080/17470218.2010.533278
- Maloney, E. A., Risko, E. F., Ansari, D. & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297. https://doi.org/10.1016/j.cognition.2009.09.013
- Maloney, E. A., Waechter, S., Risko, E. F. & Fugelsang, J. (2012). Reducing the sex difference in math anxiety: The role of spatial processing ability. Learning Individual Differences, 22(3), 380-384. https://doi.org/10.1016/j.lindif.2012.01.001
- Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58, 525-543. https://doi.org/10.1007/BF02294825
- Moses, R. P. & Cobb, C., Jr. (2001). Organizing algebra: The need to voice a demand. Social Policy, 31(4), 4-12.
- Mullis, I. V., Martin, M. O. & Foy, P. (2008). TIMSS 2007 International Mathematics Report. Boston College, TIMSS & PIRLS International Study Center website. https://timssandpirls.bc.edu/TIMSS2007/PDF/TIMSS2007_InternationalMathematicsReport.pdf
- Mullis, I. V., Martin, M. O., Foy, P. & Arora, A. (2012). TIMSS 2011 International Results in Mathematics. Boston College, TIMSS & PIRLS International Study Center website. https://timssandpirls.bc.edu/timss2011/downloads/T11_IR_Mathematics_FullBook.pdf
- Mullis, I. V., Martin, M. O., Foy, P. & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Boston College, TIMSS & PIRLS International Study Center website. http://timssandpirls.bc.edu/timss2015/international-results/timss-2015/mathematics/student-achievement/
- Mullis, I. V., Martin, M. O., Foy, P., Kelly, D. L. & Fishbein, B. (2020). TIMSS 2019 International Results in Mathematics and Science. Boston College, TIMSS & PIRLS International Study Center website. https://timss2019.org/reports/wp-content/themes/timssandpirls/download-center/TIMSS-2019-International-Results-in-Mathematics-and-Science.pdf
- Mullis, I. V., Martin, M. O. Gonzalez E. J. & Chrostowski S. J. (2004). TIMSS 2003 International Mathematics Report Findings From IEA’s Trends in International Mathematics and Science Study at the Fourth and Eighth Grades. Boston College, TIMSS & PIRLS International Study Center website. https://timssandpirls.bc.edu/PDF/t03_download/T03INTLSCIRPT.pdf
- Muthén, L. K. & Muthén, B. O. (2017). Mplus User’s guide (8e éd.). Muthén & Muthén.
- O’Grady, K., Deussing, M.-A., Scerbina, T., Fung, K. & Muhe, N. (2016). À la hauteur : Résultats canadiens de l’étude PISA de l’OCDE – Le rendement des jeunes du Canada en sciences, en lecture et en mathématiques - Premiers résultats de 2015 pour les jeunes du Canada âgés de 15 ans. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/365/PISA2015-CdnReport-FR.pdf
- O’Grady, K., Deussing, M.-A., Scerbina, T., Tao, Y., Fung, K., Elez, V. & Monk, J. (2019). À la hauteur : Résultats canadiens de l’étude PISA 2018 de l’OCDE – Le rendement des jeunes de 15 ans du Canada en lecture, en mathématiques et en sciences. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/396/PISA2018_PublicReport_FR.pdf
- OCDE (2005a), Apprendre aujourd’hui, réussir demain : Premiers résultats de PISA 2003. Éditions OCDE. https://doi.org/10.1787/9789264007260-fr
- OCDE (2005b). PISA 2003 Technical Report. Éditions OCDE. https://doi.org/10.1787/9789264010543-en
- OCDE (2009). PISA Data Analysis Manual: SPSS and SAS, Second Edition. https://doi.org/10.1787/9789264056275-en
- OCDE (2014a). Résultats du PISA 2012 : Savoirs et savoir-faire des élèves (vol. I). Éditions OCDE. https://doi.org/10.1787/9789264208827-fr
- OCDE (2014b). Résultats de PISA 2012 : Des élèves prêts à apprendre (vol. III). Éditions OCDE. https://doi.org/10.1787/9789264205345-fr
- OCDE (2014c). PISA 2012 Technical Background. Éditions OCDE.
- OCDE (2014d). L’Évaluation des compétences des adultes : Manuel à l’usage des lecteurs. Éditions OCDE. https://doi.org/10.1787/9789264204126-fr
- OCDE (2016). Résultats du PISA 2015 : L’excellence et l’équité dans l’éducation (vol. 1). Éditions OCDE. https://doi.org/10.1787/9789264267534-fr
- Park, D., Ramirez, G. & Beilock, S. L. (2014). The role of expressive writing in math anxiety. Journal of Experimental Psychology: Applied, 20(2), 103-111. https://doi.org/10.1037/xap0000013
- Parsons, S. & Bynner, J. (2005). Does numeracy matter more? National Research and Development Centre for Adult Literacy and Numeracy.
- Passolunghi, M. C., De Vita, C. & Pellizzoni, S. (2020). Math anxiety and math achievement: The effects of emotional and math strategy training. Developmental science, 23(6), e12964. https://doi.org/10.1111/desc.12964
- Paulhus, D. L. (2017). Socially desirable responding on self-reports. Encyclopedia of personality and individual differences, 1(5).
- Pekrun, R. (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational Psychology Review, 18, 315-341. https://doi.org/10.1007/s10648-006-9029-9
- Peterson, P. E., Hanushek, E. A. & Riddell, J. B. (2011, 17 août). US proficiency in math and reading lags behind that of most industrialized nations, endangering long term economic growth. Education Next, 1-2. https://www.educationnext.org/files/ednext_20114_Proficiency_PR.pdf
- Pletzer, B., Wood, G., Scherndl, T., Kerschbaum, H. H. & Nuerk, H. C. (2016). Components of mathematics anxiety: Factor modeling of the MARS30-Brief. Frontiers in psychology, 7, Article 91, 1-14. https://doi.org/10.3389/fpsyg.2016.00091
- Pronovost, M., Cormier, C., Potvin, P. & Riopel, M. (2017, 10 mai). Intérêt et motivation des jeunes pour les sciences [communication orale]. Journée de la recherche sur la motivation au collégial [colloque], Congrès de l’ACFAS, Montréal, Québec, Canada. https://eduq.info/xmlui/bitstream/handle/11515/34831/pronovost-cormier-potvin-riopel-interet-motivation-jeunes-sciences-article-acfas-2017.pdf
- Ramirez, G., Shaw, S. T. & Maloney, E. A. (2018). Math anxiety: Past research, promising interventions, and a new interpretation framework. Educational Psychologist, 53(3), 145-164. https://doi.org/10.1080/00461520.2018.1447384
- Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests, Nielsen and Lydiche.
- Reyna, V. F. & Brainerd, C. J. (2007). The importance of mathematics in health and human judgment: Numeracy, risk communication, and medical decision making. Learning and Individual Differences, 17(2), 147-159. https://doi.org/10.1016/j.lindif.2007.03.010
- Richardson, F. C. & Suinn, R. M. (1972). The mathematics anxiety rating scale: psychometric data. Journal of Counseling Psychology, 19(6), 551-554. https://doi.org/10.1037/h0033456
- Rivera-Batiz, F. L. (1992). Quantitative literacy and the likelihood of employment among young adults in the United States. Journal of Human Resources, 27(2), 313-328. https://doi.org/10.2307/145737
- Robinson, M. D. & Clore, G. L. (2002). Belief and feeling: Evidence for an accessibility model of emotional self-report. Psychological Bulletin, 128(6), 934–960. https://doi.org/10.1037/0033-2909.128.6.934
- Rossi, S., Xenidou-Dervou, I., Simsek, E., Artemenko, C., Daroczy, G., Nuerk, H. C. & Cipora, K. (2022). Mathematics–gender stereotype endorsement influences mathematics anxiety, self-concept, and performance differently in men and women. Annals of the New York Academy of Sciences, 1513(1), 121-139. https://doi.org/10.1111/nyas.14779
- Rutkowski, L., Gonzalez, E., Joncas, M. & von Davier, M. (2010). International large-scale assessment data: Issues in secondary analysis and reporting. Educational Researcher, 39(2), 142-151. https://doi.org/10.3102/0013189X10363170
- Sandman, R. S. (1980). The Mathematics attitude inventory: Instrument and user’s manual. Journal for Research in Mathematics Education, 11(2), 148-149.
- Skinner, C. & Wakefield, J. (2017). Introduction to the design and analysis of complex survey data. Statistical Science, 32(2), 165-175. https://doi.org/10.1214/17-STS614
- Sörbom, D. (1974). A general method for studying differences in factor means and factor structure between groups. British Journal of Mathematical and Statistical Psychology, 27(2), 229-239. https://doi.org/10.1111/j.2044-8317.1974.tb00543.x
- Spence, S. H. (1997). Spence children’s anxiety scale. Journal of Anxiety Disorders. https://psycnet.apa.org/doi/10.1037/t10518-000
- Stapleton, L. M. (2013). Multilevel structural equation modeling with complex sample data. Dans G. R. Hancock & R. O. Mueller (dir.), Quantitative methods in education and the behavioral sciences: Issues, research, and teaching. Structural equation modeling: A second course (p. 521–562). IAP Information Age Publishing.
- Steenkamp, J. B. E. & Baumgartner, H. (1998). Assessing measurement invariance in cross-national consumer research. Journal of consumer research, 25(1), 78-90. https://doi.org/10.1086/209528
- Steinmetz, H. (2011). Estimation and comparison of latent means across cultures. Dans Davidov, P. Schmidt & J. Billiet (dir.), Cross-cultural analysis: Methods and applications (p. 85–116). Routledge/Taylor & Francis Group.
- Stoet, G., Bailey, D. H., Moore, A. M. & Geary, D. C. (2016). Countries with higher levels of gender equality show larger national sex differences in mathematics anxiety and relatively lower parental mathematics valuation for girls. PloS One, 11(4), Article e0153857. https://doi.org/10.1371/journal.pone.0153857
- Stokke, A. (2015). What to do about Canada’s declining math scores? C.D. Howe Institute Commentary 427. https://doi.org/10.2139/ssrn.2613146
- Suárez-Pellicioni, M., Núñez-Peña, M. I. & Colomé, À. (2016). Math anxiety: A review of its cognitive consequences, psychophysiological correlates, and brain bases. Cognitive, Affective, Behavioral Neuroscience, 16(1), 3-22. https://doi.org/10.3758/s13415-015-0370-7
- Suinn, R. M. & Edwards, R. (1982). The measurement of mathematics anxiety: The Mathematics Anxiety Rating Scale for Adolescents—MARS-A. Journal of Clinical Psychology, 38(3), 576–580. https://doi.org/10.1002/1097-4679(198207)38:3<576::AID-JCLP2270380317>3.0.CO;2-V
- Supekar, K., Iuculano, T., Chen, L. & Menon, V. (2015). Remediation of childhood math anxiety and associated neural circuits through cognitive tutoring. Journal of Neuroscience, 35(36), 12574-12583. https://doi.org/10.1523/JNEUROSCI.0786-15.2015
- Szczygiel, M. (2020). Gender, general anxiety, math anxiety and math achievement in early school-age children. Issues in Educational Research, 30(3), 1126-1142. https://search.informit.org/doi/10.3316/informit.465488906598804
- Thomas, G. & Dowker, A. (2000, September). Mathematics anxiety and related factors in young children. Dans British Psychological Society Developmental Section Conference.
- Vandenberg, R. J. & Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational research methods, 3(1), 4-70.
- Vohl, P. (2023). Étude des écarts d’anxiété mathématique selon le genre et des facteurs ayant le potentiel de les réduire, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012 [thèse de doctorat, Université de Montréal]. Papyrus. https://papyrus.bib.umontreal.ca/xmlui/handle/1866/32456
- Vohl, P. & Loye N. (sous presse). Les défis liés à l’analyse secondaire de données issues des évaluations à grande échelle en éducation. Dans N. Loye & N. Duroisin (dir.), Évaluation des apprentissages et technologies numériques : évolution, nouveautés et défis actuels. Peter Lang.
- Vohl, P. & Loye, N. (2024, accepté). Étude visant à identifier des facteurs ayant le potentiel de réduire les écarts d’anxiété mathématique observés entre les garçons et les filles francophones de 15 ans du Québec, à partir d’une analyse secondaire des données issues du PISA de 2003 et de 2012. Mesure et évaluation en éducation.
- Wang, M. T., Eccles, J. S. & Kenny, S. (2013). Not lack of ability but more choice: Individual and gender differences in choice of careers in science, technology, engineering, and mathematics. Psychological science, 24(5), 770-775. https://doi.org/10.1177/0956797612458937
- Wang, J. & Wang, X. (2020). Structural equation modeling: Applications using Mplus. John Wiley & Sons.
- Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54(3), 427-450. https://doi.org/10.1007/BF02294627
- Winne, P. H. & Jamieson-Noel, D. (2002). Exploring students’ calibration of self reports about study tactics and achievement. Contemporary Educational Psychology, 27(4), 551-572.
- Zhang, J., Zhao, N. & Kong, Q. P. (2019). The relationship between math anxiety and math performance: A meta-analytic investigation. Frontiers in psychology, 10(1613), 1-17. https://doi.org/10.3389/fpsyg.2019.01613
List of tables
Tableau 1
Étude de l’invariance de la mesure d’anxiété mathématique entre les filles et les garçons francophones du Québec, pour 2003 et pour 2012
Tableau 2
Étude de l’invariance de la mesure d’anxiété mathématique pour les filles francophones du Québec entre 2003 et 2012 et pour les garçons francophones du Québec entre 2003 et 2012
Tableau 3
Pourcentage des participants qui se sont dits tout à fait en accord ou en accord avec les items de l’instrument d’anxiété mathématique en 2003 et en 2012
Tableau 4
Niveau moyen d’anxiété mathématique chez les participants du PISA de 2003 et du PISA de 2012, selon le genre, écarts selon le genre et tendance 2003-2012 des écarts selon le genre
Tableau 5
Écarts du niveau moyen d’anxiété mathématique chez les participants du PISA de 2003 et du PISA de 2012, selon le genre, à chacun des niveaux de compétence de l’échelle de compétence du PISA
Tableau 6
Résultats du premier modèle de régression linéaire chez l’ensemble des élèves québécois francophones ayant participé au PISA de 2003 et de 2012
Tableau 7
Résultats du second modèle de régression linéaire chez l’ensemble des élèves québécois francophones ayant participé au PISA de 2003 et de 2012
Note. β0= valeur estimée de l’ordonnée à l’origine, β1= valeur estimée du coefficient de régession de la variable anxiété mathématique, β2= valeur estimée du coefficient de régression de la variable genre, β3= valeur estimée du coefficient de régression de l’interaction des variables anxiété mathématique et genre, Er.t. = erreur type, p = valeur p, R2= coefficient de détermination, ANXMAT = anxiété mathématique.