Introduction au calcul de la taille d’effet globale d’une intervention dans les méta-analyses en sciences de l’éducation

Roques, Nathalie

doi:https://doi.org/10.7202/1106852ar

Introduction

De nombreuses études par comparaison de groupes ont été menées en sciences de l’éducation ces 60 dernières années dans le but de mesurer les influences d’une pratique liée à l’enseignement (comme une méthode pédagogique ou l’utilisation d’un manuel scolaire ou d’une application déployée sur ordinateur) sur ce que les élèves apprennent (Hedges & Schauer, 2018). Quand plusieurs études de ce type analysent les effets d’une même intervention, synthétiser leurs résultats permet alors d’évaluer l’efficacité globale de cette dernière. Cette information intéresse bien évidemment les acteurs de la communauté éducative, mais également les scientifiques qui orientent leurs recherches en se basant sur les résultats de travaux antérieurs. Les synthèses qui font appel à des procédures statistiques sont des méta-analyses (terme utilisé pour la première fois en 1976 par Gene Glass qui le définit comme une « analyse d’analyses »). Leurs réalisations s’appuient sur un cadre conceptuel et méthodologique qui a fait l’objet de nombreuses recherches menées en grande partie aux États-Unis (Chalmers, 2015 ; Pigott & Polanin, 2020). Des organismes comme le What Works Clearinghouse (WWC) aux USA et la Education Endowment Foundation (EEF) au Royaume-Uni ont également contribué au développement de ce pan de la recherche en publiant de nombreux documents[1] qui encadrent la réalisation de leurs méta-analyses. Les résultats de ces dernières sont également des éléments d’information importants que les praticiens comme les pouvoirs publics ne peuvent pas négliger (voir par exemple la traduction d’un Guide des Pratiques du WWC (Roques, 2022a)).

L’objectif de cet article est de faciliter la compréhension des procédures mises en oeuvre dans les méta-analyses de manière à ce qu’un large public soit capable d’en interpréter correctement les résultats et, au-delà, d’améliorer les pratiques d’analyse pour une science de l’éducation de qualité accrue. Si ces procédures sont bien documentées dans de nombreux textes anglo-saxons, bien peu d’informations sont disponibles en français. Ce texte devrait contribuer à combler cette lacune.

Une présentation générale des méta-analyses

Il faut distinguer deux niveaux de recherche. Le premier concerne les études qui comparent en milieu scolaire ordinaire deux groupes d’élèves, un groupe pour lequel une intervention est mise en place (le groupe intervention) et un groupe qui n’est pas soumis à cette intervention (le groupe témoin) : ce sont des études par comparaison de groupes. Cette catégorie regroupe des essais contrôlés randomisés (ECR), où la répartition des élèves dans les deux groupes est aléatoire, et des études quasi-expérimentales quand cette répartition n’est pas aléatoire. Certaines méta-analyses sélectionnent également des études par régression de la discontinuité ou des études de cas, mais elles sont moins fréquemment rencontrées et nous les laisserons de côté ici. D’autres types d’études sont par contre systématiquement exclus des méta-analyses, comme les études qui n’évaluent l’intervention que sur un seul groupe d’élèves (sans groupe témoin).

Quand plusieurs études indépendantes ont été menées sur une même question de recherche (ce sont les études primaires), on passe ensuite au deuxième niveau de recherche en réalisant une méta-analyse (qui est une étude secondaire). Ces deux niveaux de recherche utilisent les mêmes concepts théoriques pour conduire une analyse statistique des données et ont un même objectif : caractériser l’effet d’une intervention sur les élèves.

Les méta-analyses sont réalisées en suivant trois étapes majeures : 1) l’identification, la sélection et l’évaluation des études primaires, 2) le calcul de résultats permettant d’évaluer l’effet global d’une intervention, 3) la publication de ces résultats. La description qui suit reprend les grandes lignes directrices encadrant la réalisation des méta-analyses conduites par le WWC (2022).

La première étape : l’identification, la sélection et l’évaluation des études analysant une même intervention

Des critères sont clairement définis et énoncés a priori (en amont de l’examen des études) de manière à ce que l’identification, la sélection et l’évaluation des études soient transparentes, systématiques et exhaustives. Les motifs d’exclusion sont explicités et la liste des études exclues est publiée. Par exemple, le WWC classe les résultats des études identifiées en trois catégories : les résultats conformes sans réserve aux normes WWC, les résultats conformes avec réserve aux normes WWC ou les résultats non conformes aux normes WWC. Les résultats des études non conformes seront exclus de la méta-analyse. Nous verrons par la suite que l’évaluation des études retenues (les études conformes aux normes WWC) aura un impact sur la caractérisation de l’effet de l’intervention.

La deuxième étape : la synthèse et l’interprétation des données

L’analyse statistique des données (qui sont les résultats publiés par les études primaires sélectionnées) peut alors débuter. Dans un premier temps et pour chacune des études sélectionnées, une taille d’effet est calculée; elle quantifie l’ampleur de l’effet de l’intervention sur les élèves mesurée par l’étude. Les tailles d’effet de chacune des études sont ensuite agrégées et une taille d’effet globale est calculée. Toutes ces tailles d’effet (calculées au niveau de chacune des études mais aussi au niveau de leur ensemble) sont ensuite transformées en indicateurs plus simples à comprendre dans le but d’en faciliter l’interprétation. Cet article détaillera plus particulièrement cette deuxième étape.

La troisième étape : la publication des résultats

Les résultats statistiques sont enfin publiés sur des sites internet conçus pour s’adresser au grand public. Il est également possible de télécharger des rapports qui détaillent les procédures et les méthodes suivies, pour ceux qui souhaitent en savoir plus. Ce troisième point distingue nettement les méta-analyses des analyses primaires (d’audience le plus souvent restreinte à un cercle réduit de chercheurs) dont elles sont le fruit. Les sites internet comme Find What Works du WWC et Education Endowment Foundation sont de bons exemples de cet effort de communication.

L’ensemble des concepts et des méthodes mis en oeuvre pour réaliser des méta-analyses dans le domaine des sciences de l’éducation sont explicités de manière complète et détaillée dans The Handbook of Research Synthesis and Meta-Analysis (Cooper et al., 2019). Pour aller à l’essentiel, la lecture de Introduction to Meta-Analysis (Borenstein et al., 2009) permet de saisir le cadre méthodologique qui soutient la réalisation de ces synthèses quantitatives et plus particulièrement de comprendre les procédures statistiques déployées, mais aussi le sens à donner aux résultats. Les nombreux exemples résolus (pour lesquels des fichiers csv sont téléchargeables sur le site internet www.meta-analysis.com) font de cet ouvrage un outil pédagogique particulièrement utile aux néophytes. Enfin, la dernière version du WWC Procedures and Standards Handbook 5.0 (WWC, 2022) présente de façon claire et synthétique l’ensemble des formules applicables aux résultats des études sélectionnées dans ses annexes F et G.

Cet article n’a d’autre vocation que de proposer une initiation à certaines procédures d’analyse statistique en limitant volontairement leur champ d’application à des situations très simples. Les équations présentées ci-dessous qui permettent de calculer les estimations ponctuelles des tailles d’effet et d’estimer leur précision, dans un premier temps pour une étude primaire, puis pour en ensemble de ces études, ne permettent pas de traiter l’ensemble des questions auxquelles un méta-analyste doit faire face. Pour relever ce défi, une expertise professionnelle basée sur des connaissances approfondies en analyse statistique mais aussi sur une solide expérience du terrain est indispensable.

La taille d’effet d’une étude primaire

Dans ce qui suit, les données brutes exploitées par les études primaires sélectionnées sont des scores d’élèves obtenus après passation d’un test à la fin de l’expérience, ou scores post-tests (ce sont des données continues). Il s’agit d’un cas simple où les élèves sont affectés dans l’un des deux groupes au niveau individuel et où les scores ne sont pas ajustés à des covariables. Dans la plupart des études de grande ampleur, des classes ou des établissements sont affectés dans ces deux groupes et les scores post-tests sont ajustés aux scores prétests (scores des élèves obtenus avant l’intervention). Cette complexité du terrain est évoquée en fin d’article où des pistes qui permettent d’en tenir compte sont proposées. Afin de comparer puis de synthétiser tous ces résultats, il est indispensable de produire dans un premier temps un indicateur commun pour chacune des études : la taille d’effet. Considérons deux échantillons. L’échantillon a subit l’intervention dont nous cherchons à évaluer les bénéfices (c’est le groupe intervention) et l’échantillon b ne subit pas l’intervention (c’est le groupe témoin). Nous sommes dans la situation où les tailles d’échantillon n_a et n_b, les moyennes m_a et m_b ainsi que les écart-types s_a et s_b des scores post-tests des élèves des deux groupes, sont connus. Ces échantillons sont représentatifs de deux populations, la population a (la population traitée, qui est une population fictive) et la population b (la population non traitée qui est la population réelle). Au niveau de ces populations, μ_a et μ_b sont les moyennes des scores post-tests et σ leur écart-type[2]. Ces nombres sont des paramètres de ces populations et ne sont pas connus des chercheurs. Par définition, la taille d’effet de l’intervention au niveau de la population (aussi nommée taille d’effet réelle) est la différence des moyennes standardisée, c’est-à-dire la différence entre les deux moyennes, divisée par l’écart-type des populations. Cela revient à déterminer la différence des moyennes comme un nombre d’écarts-types. Ce paramètre est noté δ

Comme toujours en statistiques inférentielles, nous cherchons à estimer ce paramètre à partir des observations faites sur les deux échantillons et à évaluer la qualité de cette estimation. Pour répondre à la première demande, nous calculons une estimation ponctuelle de la taille d’effet réelle ; pour répondre à la seconde demande, nous calculons l’erreur type de cette estimation et l’intervalle de confiance à 95 % qui pourra lui être associé.

Les estimations ponctuelles d’une taille d’effet

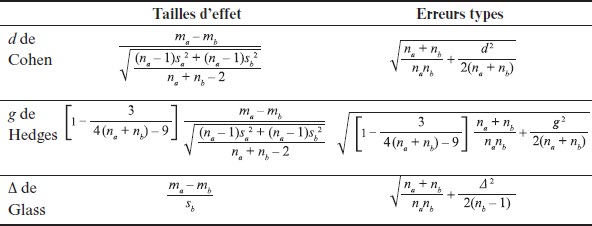
Les moyennes des populations seront estimées par les moyennes des échantillons m_a et m_b. Notons que c’est la différence des moyennes qui intéresse le chercheur ici et, dans les études utilisant un modèle de régression linéaire multiple, cette différence est égale au coefficient de corrélation de la variable indicatrice « intervention ». En ce qui concerne l’estimation de l’écart-type de la population σ, deux méthodes de calcul sont utilisées et ont donné naissance à deux familles d’estimations de δ : le d de Cohen (Cohen, 1988) et le g de Hedges (Hedges, 1981), d’une part, le Δ de Glass (Glass & Smith, 1977), d’autre part. Les dénominations fluctuent d’un article à l’autre : dans le cas présent, les définitions utilisées par Borenstein et al. (2009) ont été employées. Pour les deux premières, c’est l’utilisation (ou non) d’un facteur correctif pour des échantillons de petite taille qui fera la différence.

Quand il est raisonnable de penser que les écarts-types des groupes intervention et témoin sont des estimations de l’écart-type de la population, ce dernier est estimé par s l’écart-type groupé, qui est la racine carrée de la moyenne des variances pondérée par leurs degrés de liberté. Nous calculons alors d, une estimation de la taille d’effet δ :

En 1981, Hedges montre que le d de Cohen est biaisé (son espérance n’est pas égale à δ la taille d’effet de la population) et que ce biais est substantiel pour les échantillons de petites tailles[3]. L’estimation non biaisée est obtenue en multipliant d par un facteur multiplicatif correctif ω. Une nouvelle estimation de δ, le g de Hedges, ont alors obtenue :

C’est l’estimation utilisée par le WWC et EEF pour les études par comparaison de groupes utilisant des données continues avec affectation au niveau individuel. Pour des échantillons de grande taille, le facteur correctif ω est très proche de 1 et est souvent négligé.

Quand l’écart-type du groupe témoin (le groupe b) est une bonne estimation de l’écart-type de la population ou quand les écarts-types des groupes témoin et intervention sont très différents (et que l’écart-type groupé ne semble pas estimer correctement l’écart-type de la population), alors le Δ de Glass est utilisé pour estimer la taille de l’effet δ

Ce choix se justifie aussi en soulignant que, dans les études par comparaison de groupes, l’intervention influe sur la moyenne des scores, bien sûr, mais également sur leur écart-type, et qu’il est dans ce cas préférable d’utiliser l’écart-type du groupe témoin comme estimation de l’écart-type de la population. C’est par exemple l’option retenue par Slavin et al. (2009) dans leur méta-analyse sur les méthodes pédagogiques efficaces pour l’enseignement des mathématiques.

Exemple numérique (1/4)

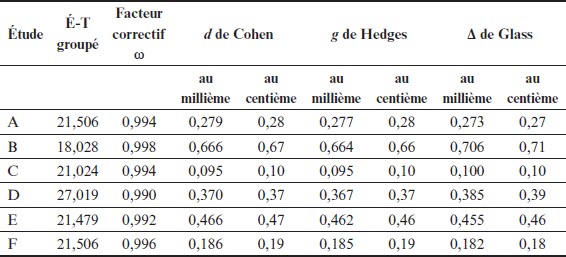
Cet exemple est inspiré de Borenstein et al. (2009, p. 88). Il a été partagé en quatre parties pour suivre au mieux le texte. Le tableau 1 présente les données fictives de six études repérées par les lettres A à F. Il est possible de télécharger un fichier Excel sur www.mathadoc.fr (à consulter notamment pour les questions d’arrondis)[4]. Les résultats sont donnés au millième près, ou sont des valeurs exactes.

Tableau 1

***Données de six études fictives***

Les calculs du d de Cohen, du g de Hedges, du Δ de Glass pour l’étude A

Le calcul des tailles d’effet s’effectue selon les trois méthodes vues ci-dessus. Il faut obtenir l’écart-type groupé s pour calculer le d de Cohen et le g de Hedges :

ω le terme correctif qui permet de calculer le g de Hedges, s’obtient de la façon suivante :

Pour calculer le Δ de Glass, il faut diviser la différence des moyennes par l’écart-type du groupe témoin :

Finalement, les résultats sont rassemblés dans le tableau 2 (les taille d’effet sont également présentées avec un arrondi au centième, précision communément adoptée dans les articles publiant les résultats de méta-analyses).

Tableau 2

***Tailles d’effet de six études fictives***

Ici, les trois méthodes de calcul donnent pour une même étude des tailles d’effet différentes de 0,05 au plus (c’est le cas de l’étude B). Avec un arrondissement au dixième près, plus aucune différence n’est décelable.

Le calcul des erreurs types

L’erreur type de l’estimation d’un paramètre est l’écart-type de sa distribution d’échantillonnage (par exemple imaginons qu’un grand nombre d’expériences sont faites, toutes de la même manière, et qu’un grand nombre d’estimations de la taille d’effet sont calculées à partir des observations).

Nous calculons une variance de la distribution d’échantillonnage de chacune des trois estimations d, g, et Δ,.

La variance du d de Cohen (notée V_d) est

Le premier terme reflète l’incertitude dans l’estimation de la différence des moyennes, le second reflète l’incertitude dans l’estimation de l’écart-type σ. Et comme g = ωd, nous calculons alors la variance de g (notée V_g)[5]

Par définition ω < 1 donc ω² < 1 et V_g < V_d. Cela signifie que la précision du g de Hedges est supérieure à la précision du d de Cohen.

Et enfin, pour le Δ de Glass, la variance de Δ notée V_Δ se calcule comme suit :

Il faut remarquer que 2 (n_b– 1) < 2 (n_a + n_b) et que V_Δ > V_d > V_g.

Notons enfin que pour toutes ces variances, plus les échantillons sont de tailles importantes, plus les variances sont faibles et la précision des estimations des tailles d’effet augmente.

Les racines carrées de ces variances permettent alors de calculer les écarts-types de ces estimateurs, qui sont des erreurs types s_d,s_g et s_Δ. Le tableau 3 récapitule les différentes formules de ce chapitre.

Tableau 3

***Tailles d’effet et erreurs types pour les trois méthodes de calcul***

Comme nous venons de le voir, le g de Hedges est non-biaisé et sa variance est la plus petite. C’est ce qui explique qu’il soit choisi pour estimer les tailles d’effet dans presque toutes les études par comparaison de groupes récentes. Dans la suite de cet article, seules les méthodes et les formules utilisant le g de Hedges seront présentées.

L’estimation par intervalle de confiance et test d’hypothèse

Nous verrons plus loin que la précision des tailles d’effet a toute son importance quand il s’agit de caractériser l’effet d’une intervention.

La distribution du g de Hedges est une loi de Student non centrée asymétrique qu’il est possible d’approcher par une loi normale pour des degrés de liberté suffisamment grands (Hedges, 1981). Ainsi, δ est estimé en calculant un intervalle de confiance à 95 %

Si cet intervalle ne contient pas la valeur zéro, nous pourrons conclure à un effet statistiquement significatif au niveau de confiance 0,95. Dans le cas contraire, nous dirons que le résultat est statistiquement non significatif. Cette présentation dichotomique des résultats utilisée par le WWC peut prêter à discussion. Par exemple, la EEF a abandonné cette classification en 2022 (EEF, 2022 ; Roques, à paraître) et se contente de donner l’estimation ponctuelle accompagnée de son intervalle de confiance (dénommé intervalle de compatibilité) sans autre commentaire. Dans la suite de cet article qui s’appuie largement sur les procédures statistiques déployées et publiées par le WWC, les résultats seront présentés comme statistiquement significatifs (ou non).

Il est également possible de suivre la procédure des tests d’hypothèse pour estimer la signification statistique à associer au g de Hedges. Ici, un test Z sera conduit pour décider s’il est possible d’écarter l’hypothèse nulle H₀ qui est « la taille d’effet au niveau de la population est égale à zéro », ou encore « δ = 0 ». Pour des échantillons de tailles suffisamment grandes, la variable centrée réduite suit une loi normale centrée-réduite sous H₀. La valeur observée Z_obs est comparée à la valeur critique au niveau de confiance choisi (p. ex., pour un risque de première espèce α = 0,05, z_obs, est comparée à 1,96 et à –1,96). La valeur –p correspondante est également calculée et comparée à α.[6]

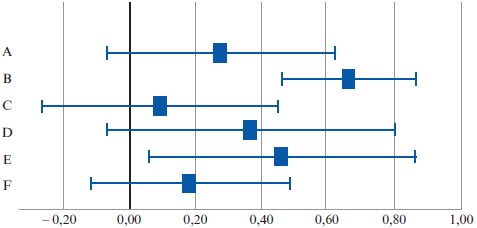
Enfin, les résultats sont représentés par un diagramme en forêt. L’axe des abscisses est gradué en nombre de tailles d’effet. Pour chaque étude, l’estimation de la taille d’effet (carré noir) et son intervalle de confiance à 95 %, qui est représenté par un segment, sont présentés sur une ligne (voir la figure 1 de l’exemple numérique).

Exemple numérique (2/4)

Le calcul des variances et des intervalles de confiance

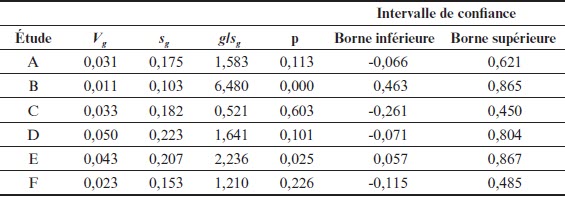
Nous nous intéresserons d’abord à l’étude A pour calculer les bornes de l’intervalle de confiance et la valeur –p associée au test Z avec α = 0,05. La variance de g est calculée :

Nous calculons une valeur –p égale à 0,113. La taille d’effet calculée est statistiquement non significativement différente de 0. L’intervalle de confiance au seuil de 0,95 est [– 0,066 ; 0,621] qui inclut la valeur 0.

Pour l’étude B, le g de Hedges et sa variance sont calculés de la même façon :

Ici, la taille d’effet est statistiquement et significativement différente de 0 (valeur –p < 0,001) et l’intervalle de confiance au seuil de 0,95 qui est [0,463 ; 0,865] n’inclut pas la valeur 0.

Les résultats des six études fictives sont rassemblés dans le tableau 4. Pour la moitié des études, l’intervalle de confiance inclut la valeur 0 et les tailles d’effet sont statistiquement non significatives (ce qui correspond à une valeur-p supérieure à 0,05).

La figure 1 représente ces résultats sous la forme d’un diagramme en forêt. Les résultats non significatifs sont ceux pour lesquels l’intervalle de confiance est coupé par la droite verticale passant par 0.

Tableau 4

***Intervalles de confiance des tailles d’effet des six études fictives***

Figure 1

***g de Hedges et intervalles de confiance pour les six études fictives***

Les méta-analyses

Nous supposons ici que des études primaires indépendantes ont été sélectionnées et que chacune d’entre elles a donné lieu au calcul d’une taille d’effet comme nous venons de le voir. C’est le cas le plus simple. Une étude peut parfois donner lieu au calcul de plusieurs tailles d’effet et, dans ce cas, ces tailles d’effet ne sont pas indépendantes. Cette situation requiert un traitement particulier qui est en dehors des objectifs de cet article.

Le but poursuivi par le méta-analyste est de même nature que celui que poursuit l’auteur d’une étude primaire : calculer un indicateur de position centrale qui est l’estimation d’un paramètre de la population (p. ex., la moyenne des scores pour les études primaires) et évaluer la dispersion des données autour de cet indicateur (comme l’écart-type des scores pour le premier type d’études). Les statisticiens conduisant les méta-analyses publiées par des organismes tels que la EEF, le Center for Research and Reform in Education (bestevidence.org/) ou l’organisation Campbell (www.campbellcollaboration.org/) utilisent tous le modèle des effets aléatoires. Ce modèle statistique peut être considéré comme une amélioration du modèle de l’effet fixe qui a l’avantage d’être plus simple à comprendre. C’est pour cette raison que ce chapitre débute par une présentation du modèle de l’effet fixe, qui n’est pas celui qui nous intéresse réellement. Si la liste des organismes cités ci-dessus n’inclut pas le WWC, c’est tout simplement que leurs méta-analyses ne comptent pas suffisamment d’études pour appliquer le modèle des effets aléatoires (voir plus loin).

Dans ce qui suit, k études partageant des caractéristiques communes, comme l’intervention étudiée et les compétences testées, ont été publiées. Pour chaque étude i (compris entre i = 1 et k), une taille d’effet a été calculée et est ici le g de Hedges. Pour l’étude i, la taille d’effet est notée g_i, sa variance V_gi et son erreur type s_gi ; n_ai et n_bi désignent les tailles d’échantillons des groupes intervention et contrôle et N_i la taille totale de l’échantillon de l’étude i ; donc N_i = n_ai + n_bi.

Le modèle de l’effet fixe

Ce modèle ne peut être appliqué que si les études sélectionnées ont toutes été menées dans des conditions similaires, sur des populations identiques ayant subi une même intervention. La plupart du temps, les études sélectionnées par une méta-analyse en sciences de l’éducation ne satisfont pas à ces critères, mais comprendre ce modèle permettra de comprendre le modèle des effets aléatoires présenté plus loin. Dans cette situation qui peut être qualifiée de théorique, les études sont des répétitions d’un même protocole qui permet d’estimer une seule et unique taille d’effet réelle δ c’est-à-dire la taille d’effet de l’intervention sur la population entière dont sont issus les échantillons. Les différences observées entre les tailles d’effet expérimentales ou quasi-expérimentales sont donc le fruit du hasard qui prévaut dans tout échantillonnage. La taille d’effet globale notée M, estimation de la taille d’effet réelle unique δ, est calculée. De la même façon que pour une étude primaire, la variance de cette taille d’effet globale (notée V_M) est également calculée pour définir un intervalle de confiance ou pour procéder à un test d’hypothèse. Ces derniers éléments auront toute leur importance quand il s’agira de caractériser l’effet de l’intervention.

La taille d’effet globale M calculée en utilisant le modèle de l’effet fixe est égale à la moyenne des tailles d’effet calculées pour chacune des études, pondérée par les inverses de leur variance qui sont donc les poids affectés à chaque étude (noté P_i)[7].

Plus la variance de la taille d’effet de l’étude i est faible, plus son poids dans le calcul de la taille d’effet globale est important. Il est possible de montrer que le poids de la taille d’effet de l’étude augmente si

N_i la taille totale de l’échantillon augmente,
pour une taille totale N_i fixée, les tailles des deux échantillons se rapprochent.

La variance de M et son écart-type (noté s_M) sont alors calculés.

Admettons que la statistique M est normalement distribuée. Il sera possible de mener un test Z et de déterminer si M est statistiquement et significativement différente de zéro en ayant fixé un risque α. L’hypothèse nulle est ici que « la taille d’effet réelle est nulle » ou encore « δ = 0 ». La valeur observée z_obs est calculée ainsi que la valeur –p associée.

Nous pouvons également définir un intervalle de confiance au niveau de confiance 0,95.

Si cet intervalle comprend la valeur zéro, nous conclurons à une absence de signification statistique.

Le modèle des effets aléatoires

Ce modèle est choisi quand les études primaires sélectionnées ont été menées sur des populations différentes (p. ex., d’âges ou de pays différents) en appliquant des protocoles divers (p. ex., les durées des interventions ou les designs des études sont différents). La plupart du temps, les études primaires rassemblées lors de méta-analyses réalisées dans le domaine des sciences de l’éducation sont hétérogènes et correspondent bien à cette description. C’est donc ce modèle qui est le plus souvent choisi. Dans ce cas, les différences entre les résultats expérimentaux (ou quasi-expérimentaux) obtenus d’une étude à l’autre sont attribuables comme toujours à l’échantillonnage, mais aussi aux caractéristiques diverses évoquées ci-dessus. Nous considérerons que la taille d’effet calculée pour chaque étude i estime une taille d’effet réelle unique (notée δ_i) associée aux caractéristiques particulières de l’étude i et que ces tailles d’effet réelles δ_i sont elles-mêmes normalement distribuées autour d’une taille d’effet globale réelle δ, avec un écart-type noté τ. Cette taille d’effet globale réelle δ est le paramètre que nous cherchons à estimer.

Nous devons considérer deux distributions :

la distribution normale des tailles d’effet calculées pour une étude donnée autour de la taille d’effet réelle δ_i de cette étude avec une erreur type (qui est aussi la racine carrée de la variance intra-étude) et que nous savons estimer (voir ci-dessus);
la distribution normale des tailles d’effet réelles δ_ide l’ensemble des études autour de la taille d’effet globale δ avec un écart-type τ_i (qui est aussi la racine carrée de la variance inter-études τ2), taille d’effet globale et écart-type que nous cherchons à estimer. Nous noterons ici M* et T ces estimations.

Il est déjà possible de dresser le bilan suivant concernant les notations et le vocabulaire utilisés :

Le modèle des effets aléatoires prenant en compte les différences entre les populations analysées par les études primaires, il est donc possible d’inférer au-delà de ces populations considérées ici comme des échantillons d’un ensemble plus large, ce qui n’était pas possible avec le modèle de l’effet fixe précédemment étudié.

Au niveau des calculs, les principes sont les mêmes que ceux mis en oeuvre dans le modèle de l’effet fixe et l’estimation de la taille d’effet réelle moyenne est toujours égale à la moyenne des tailles d’effet expérimentales pondérée par les inverses de leur variance. Il faudra ici rajouter aux variances intra-étude l’estimation de la variance inter-études. La variance de la taille d’effet calculée pour l’étude i dans ce modèle est notée V_gi* et la variance et l’erreur type de M* sont notées V_M* et s_M*.

Comme pour le modèle précédent, en considérant que M* est normalement distribuée, nous procédons à un test Z avec comme hypothèse nulle que « la taille d’effet moyenne de la population est égale à zéro » ou encore « δ = 0 » et en associant à ce test une valeur –p avec

Un intervalle de confiance au niveau 0,95 est aussi calculé.

Soulignons que, par définition, V_gi* ≥ V_gi, donc s_M* ≥ s_M, ce qui revient à dire que le modèle des effets aléatoires, incluant de fait la variabilité des études dans la variabilité totale, est moins précis que le modèle des effets fixes.

Il va falloir calculer T ², l’estimation de τ². Il est ici admis que :

Si Q – (k – 1) < 0, la valeur nulle sera attribuée à T ² (τ² ne peut pas être négative).

Il faut un nombre suffisant d’études pour pouvoir estimer T ² avec assez de précision[8]. Si le nombre d’études sélectionnées est trop faible, c’est le modèle de l’effet fixe qui devra être utilisé, mais il ne permettra pas d’inférer au-delà des populations analysées dans les études primaires.

Les méta-analyses réalisées par la EEF pour identifier les méthodes pédagogiques efficaces (voir les pages du Teaching and Learning Toolkit sur leur site internet) rassemblent un grand nombre d’études et utilisent le modèle des effets aléatoires pour calculer les tailles d’effet globales. Les méta-analyses du WWC, quant à elles, ne comptent le plus souvent qu’une poignée d’études primaires, car elles ne concernent qu’une seule intervention clairement identifiée et doivent respecter un cahier des charges exigeant pour être sélectionnées. La taille d’effet globale est donc calculée en suivant le modèle de l’effet fixe. Et même, si les hypothèses de départ restent celles du modèle des effets aléatoires (les tailles d’effet réelles des études primaires sont reconnues être différentes les unes des autres), les conclusions des méta-analyses du WWC ne pourront pas être étendues au-delà des populations analysées par les études sélectionnées. Ce modèle mixte a été baptisé par le WWC modèle des effets fixes (WWC, 2022).

Exemple numérique (3/4)

Les données des tableaux 2 et 4 sont utilisées pour appliquer successivement le modèle de l’effet fixe puis le modèle des effets aléatoires aux six études fictives.

Le modèle de l’effet fixe

Le poids est calculé pour chacune des études. Pour l’étude A, P = 1/0,031=32,568. Les poids des cinq autres études sont obtenus de la même façon (tableau 5).

Tableau 5

***Poids des six études fictives (modèle de l’effet fixe)***

Une valeur – p inférieure à 0,001 est alors calculée. La taille d’effet globale calculée est statistiquement et significativement différente de 0 (test Z avec α = 0,05). L’intervalle de confiance au seuil de 0,95 est [0,289 ; 0,540] qui n’inclut pas la valeur 0.

Le modèle des effets aléatoires

Il faut calculer la variance intra-étude T ². k = 6, donc k – 1 = 5

Les variances des tailles d’effet sont calculées en rajoutant à la variance intra-étude la variance inter-étude T ². Par exemple, pour l’étude A,

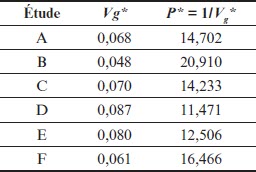
V_g* = 0,031 + 0,037 = 0,068 et P* = 1/0,068 = 14,703

Les poids des cinq autres études s’obtiennent de la même façon (tableau 6).

Tableau 6

***Poids des six études fictives (modèle des effets aléatoires)***

Nous procédons de la même façon que pour le modèle de l’effet fixe pour calculer ensuite les autres résultats.

Une valeur –p inférieure à 0,001 est alors calculée. La taille d’effet globale calculée est statistiquement et significativement différente de 0 (test Z avec α = 0,05). L’intervalle de confiance au seuil de 0,95 est [0,152 ; 0,565] qui n’inclut pas la valeur 0.

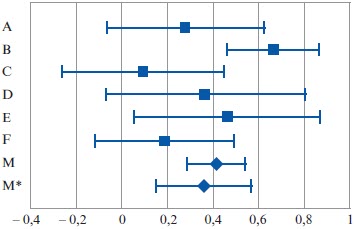
Un diagramme en forêt (figure 2) présente les résultats de ces deux méta-analyses. Les losanges noirs représentent les estimations ponctuelles des effets globaux. Il est à noter que l’intervalle de confiance de la taille d’effet est plus grand quand le modèle des effets aléatoires est choisi. Quel que soit le modèle utilisé, les intervalles de confiance des tailles d’effet des études sont calculés à partir de la variance intra-étude V_g (et non V^*_g).

Figure 2

***Intervalles de confiance des tailles d’effet des études et des tailles d’effet globales pour les deux modèles***

Le bilan

Le tableau 7 présente les éléments essentiels de ces deux modèles statistiques pour les quatre points clés suivants : les hypothèses initiales qui influent sur le choix du modèle, la modélisation des tailles d’effet réelles des études, les poids intervenant dans le calcul de la taille d’effet globale et les limites concernant les inférences.

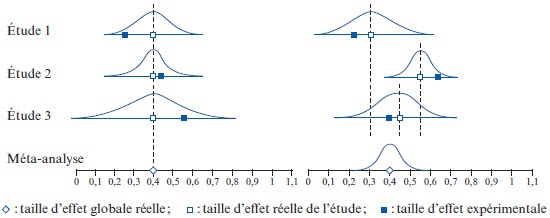
La figure 3 propose une représentation graphique des distributions normales des estimations des tailles d’effet de trois études fictives selon les deux modèles. À gauche c’est le modèle de l’effet fixe qui a été mis en oeuvre, à droite, le modèle des effets aléatoires[9]. Dans le modèle de l’effet fixe, la taille d’effet réelle est la même pour toutes les études (les carrés blancs sont sur une même ligne verticale) et c’est également la taille d’effet réelle globale (losange blanc). Dans le modèle des effets aléatoires, les tailles d’effet réelles sont différentes d’une étude à l’autre et normalement distribuées autour de la taille d’effet réelle globale.

Tableau 7

***Comparaison entre modèle de l’effet fixe et modèle des effets aléatoires***

Figure 3

***Exemple de trois études fictives (À gauche le modèle de l’effet fixe, à droite le modèle des effets aléatoires)***

Les interprétations des résultats

Comme cela a déjà été signalé au début de l’article, la finalité des synthèses des études par comparaison de groupes est avant tout de répondre aux attentes concrètes des praticiens comme des pouvoirs publics en leur permettant de trouver les interventions efficaces. La troisième étape de cette analyse statistique consiste à bâtir un pont entre les résultats statistiques qui en sont le fruit et les salles de classe. Pour faciliter cette interprétation des résultats, les tailles d’effet calculées (aussi bien pour une étude primaire que pour une méta-analyse) sont traduites en indicateurs plus intuitifs. De plus, l’effet d’une intervention est parfois classé en fonction de plusieurs paramètres comme les résultats de l’étude primaire (ou de la méta-analyse) mais aussi la qualité de l’étude primaire (ou la quantité et la qualité des études primaires sélectionnées pour une méta-analyse).

Interpréter une taille d’effet

Nous pouvons traduire la taille d’effet comme étant la différence des moyennes des deux groupes (intervention et témoin) en nombre d’écarts-types. Les personnes habituées à considérer des courbes normales peuvent déjà y voir un élément éclairant. Mais pour des personnes peu familières avec les statistiques, il existe d’autres interprétations plus compréhensibles. Certains utilisent encore la grille d’interprétation de Cohen (Cohen, 1988) qui indique qu’une taille d’effet supérieure à 0,8 est importante, qu’elle est moyenne entre 0,2 et 0,8 et faible sous ce seuil. Cette grille de lecture basée notamment sur une comparaison des tailles de jeunes filles réparties en groupes d’âge ne semble pas adaptée aux sciences de l’éducation où d’autres indicateurs sont actuellement utilisés. Par exemple, la EEF traduit la taille d’effet en un nombre de mois de progrès. Il s’agit plus précisément du nombre de mois dont un élève moyen du groupe intervention a progressé par rapport à un élève moyen du groupe témoin. La EEF considère que, pour la plupart des scores mesurés au niveau national, un élève britannique progresse de 1 écart-type en une année scolaire; donc, un mois d’études équivaut à 1/12 d’écart-type soit 0,09 écart-type. Le tableau 8, qui associe chaque nombre de mois de progrès à un intervalle des tailles d’effet, concerne les études primaires (EEF, n. d.). Un tableau légèrement différent (ces différences concernent les deux premières colonnes du tableau 8) est publié pour les tailles d’effet globales calculées pour les méta-analyses du Toolkit (EEF, 2023).

Tableau 8

***Nombre de mois de progrès pour une étude primaire***

Le WWC propose quant à lui de traduire la taille d’effet par un indice d’amélioration (IA) qui est le changement attendu du rang centile d’un élève moyen du groupe témoin qui serait ensuite soumis à l’intervention. Il peut aussi s’agir de la différence entre le rang centile d’un élève du groupe témoin qui obtient le score d’un élève moyen du groupe intervention et le rang centile d’un élève moyen du groupe témoin. Le calcul de l’indice d’amélioration se fait en deux étapes : il faut d’abord calculer l’indice U3 de Cohen, qui est la fraction des élèves du groupe témoin surpassés par l’élève moyen du groupe intervention (et qui se calcule grâce aux propriétés des courbes normales). En l’absence d’intervention, cet indice est égal à 50 %. Puis, il faut soustraire 50 % à l’indice U3.

Exemple numérique (4/4)

À partir des g de Hedges des six études de l’exemple numérique (tableau 2), les indices d’amélioration sont calculés et les nombres de mois de progrès correspondants déterminés (tableau 9).

Tableau 9

***Indices d’amélioration (IA) et nombre de mois de progrès des six études fictives (les tailles d’effet sont arrondies au centième comme cela est d’usage)***

Par exemple, pour l’étude A, nous pourrons dire que la moyenne du groupe intervention est supérieure de 0,28 écart-type à la moyenne du groupe témoin, ou que l’élève moyen du groupe intervention a progressé de 11 centiles dans la cohorte, ou qu’il a fait autant de progrès grâce à l’intervention qu’il en aurait fait sans intervention en quatre mois.

Le tableau 10 présente les résultats pour les tailles d’effet globales M et M*.

Tableau 10

***Indices d’amélioration (IA) et nombre de mois de progrès pour les tailles d’effet globales***

Caractériser l’effet d’une intervention

L’objectif ici est d’associer un niveau de preuve à l’effet tel qu’il a été calculé, aussi bien pour une étude primaire que pour une méta-analyse. La description qui suit reprend les lignes directrices encadrant l’interprétation des résultats des analyses du WWC (WWC, 2022). Nous avons déjà vu que le WWC classe les études en évaluant leur design et donc leur validité interne. Dans le cas présent, il s’agit de caractériser l’effet d’une intervention en tenant compte à la fois du design de l’étude (ou des études sélectionnées dans le cas d’une méta-analyse) mais aussi de l’ampleur de l’effet (c’est-à-dire de la taille d’effet) et de la précision avec laquelle cet effet a été évalué, par exemple en calculant un intervalle de confiance. Pour une étude primaire comme pour une méta-analyse, le WWC classe l’effet de l’intervention dans l’une des cinq catégories suivantes : 1) preuves fortes (tier 1), 2) preuves modérées (tier 2), 3) preuves prometteuses (tier 3), 4) effets incertains et 5) effets négatifs. Par exemple, pour obtenir le niveau le plus élevé, la taille d’effet (la taille d’effet globale pour une méta-analyse) doit être positive et statistiquement significative, l’échantillon total doit avoir un effectif supérieur à 350 et inclure plusieurs sites. De plus, dans le cas d’une étude primaire, celle-ci doit être conforme sans réserve aux normes WWC ; dans le cas d'une méta-analyse, les résultats d'études conformes sans réserve aux normes WWC doivent représenter plus de 50 % du poids des tailles d’effets calculées et aucun effet négatif ne doit avoir été publié. Quand une taille d’effet positive est calculée mais qu’elle n’est pas statistiquement significative, pour une étude primaire comme pour une méta-analyse, l’effet de l’intervention est classé par le WWC comme présentant des effets incertains.

5. La complexité du terrain

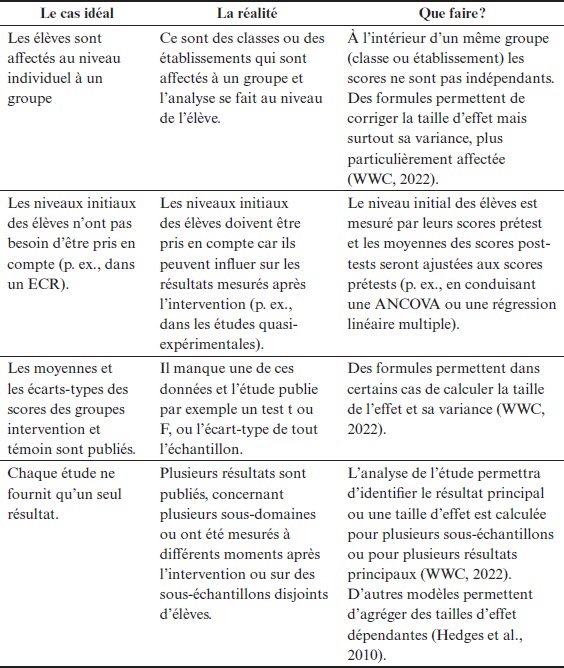
Les méthodes statistiques présentées dans cet article concernent la situation la plus simple que puisse rencontrer un chercheur :

les élèves sont affectés au niveau individuel à un groupe (intervention ou témoin),
leur niveau initial n’a pas besoin d’être pris en compte,
les moyennes et les écarts-types des scores des groupes intervention et témoin sont publiés, et
les études ne fournissent qu’un seul résultat.

Comme chacune de ces conditions est le plus souvent contredite en pratique, il faut tenir compte de la réalité du terrain. Les informations données dans le tableau 11 ci-dessous n’ont d’autre vocation que de fournir quelques pistes.

Prenons comme exemple une étude avec affectation au niveau individuel qui a mené une régression linéaire multiple permettant de tenir compte des scores prétests des élèves. Si cette étude ne publie pas les écarts-types non ajustés des groupes intervention et témoin mais le résultat d’un test t ajusté aux scores prétests ainsi que le coefficient de corrélation du modèle linéaire R², le g de Hedges pourra être calculé de la façon suivante (WWC, 2022) :

Et la variance de la taille d’effet est alors égale à

Tableau 11

***La complexité du terrain***

Conclusion

Cet article avait comme objectif de poser les règles de calcul permettant d’estimer la taille d’effet globale d’une intervention dans le cas simple d’une méta-analyse n’ayant sélectionné que des études expérimentales ou quasi-expérimentales avec affectation des élèves au niveau individuel, sans tenir compte d’éventuelles covariables. Les estimations ponctuelles et leurs variances calculées en suivant le modèle des effets aléatoires ne sont que les premiers éléments de la description quantitative d’un ensemble d’études traitant d’un sujet commun. De nos jours, les regards se tournent plus volontiers vers une analyse de l’hétérogénéité de ces indicateurs (Pigott, 2020; Roques, 2022b). En s’inspirant de modèles statistiques mis en oeuvre pour des études primaires, des analyses de sous-groupes (qui sont en fait des ANOVA) ou des méta-régressions (qui sont des régressions linéaires multiples) sont alors conduites (Tipton et al., 2018) et permettent d’explorer les influences que certaines variables modératrices peuvent avoir sur les tailles d’effet. Ces méthodes ont été mises en oeuvre par exemple dans la méta-analyse conduite par la collaboration Campbell en 2021 (Dietrichson et al., 2021) et qui porte sur l’enseignement des mathématiques et de la lecture en primaire. Nous pouvons également citer les méta-analyses menées par la EEF pour son Toolkit ou encore la méta-analyse de Slavin et al. (2009). L’objectif n’est plus alors d’analyser l’effet d’une intervention, mais d’identifier des caractéristiques (un élément spécifique commun à plusieurs interventions, par exemple, ou un domaine précis des apprentissages) associées à l’ampleur de l’effet calculé.

Les derniers mots concerneront la complexité parfois peu visible qui caractérise les procédures, les analyses statistiques et les concepts structurant les méta-analyses. La synthèse d’études quantitatives peut en effet séduire un public large de non-initiés, car elle s’apparente dans ses grandes lignes à un simple calcul de moyenne. Cette simplicité de façade représente finalement un défi pour les méta-analystes qui doivent souvent expliciter leurs procédures pour justifier de la qualité de leur synthèse (Berlin & Golub, 2014). Le WWC l’a bien compris. En effet, il exige de ses examinateurs qu’ils soient certifiés après avoir suivi une formation interne obligatoire et s’efforce de développer, de publier et de mettre à jour des documents cadres qui constituent une référence incontournable dans ce domaine.

Note de l’auteure

Résumé